摘要:9.已知棱锥的顶点为.在底面上的射影为.现用平行于底面的平面去截这个棱锥.截面交于点.并使截得的两部分侧面积相等.设.则与的关系是
网址:http://m.1010jiajiao.com/timu_id_352147[举报]
 已知四边形ABCD为菱形,AB=6,∠BAD=60°,两个正三棱锥P-ABD、S-BCD(底面是正三角形且顶点在底面上的射影是底面正三角形的中心)的侧棱长都相等,如图,E、M、N分别在AD、
已知四边形ABCD为菱形,AB=6,∠BAD=60°,两个正三棱锥P-ABD、S-BCD(底面是正三角形且顶点在底面上的射影是底面正三角形的中心)的侧棱长都相等,如图,E、M、N分别在AD、
AB、AP上,且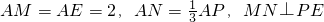 .
.
(Ⅰ)求证:PB⊥平面PAD;
(Ⅱ)求平面BPS与底面ABCD所成锐二面角的平面角的正切
值;
(Ⅲ)求多面体SPABC的体积.
查看习题详情和答案>>
已知四边形ABCD为菱形,AB=6,∠BAD=60°,两个正三棱锥P-ABD、S-BCD(底面是正三角形且顶点在底面上的射影是底面正三角形的中心)的侧棱长都相等,如图,E、M、N分别在AD、
AB、AP上,且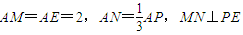 .
.
(Ⅰ)求证:PB⊥平面PAD;
(Ⅱ)求平面BPS与底面ABCD所成锐二面角的平面角的正切
值;
(Ⅲ)求多面体SPABC的体积.
 查看习题详情和答案>>
查看习题详情和答案>>
AB、AP上,且
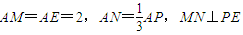 .
.(Ⅰ)求证:PB⊥平面PAD;
(Ⅱ)求平面BPS与底面ABCD所成锐二面角的平面角的正切
值;
(Ⅲ)求多面体SPABC的体积.
 查看习题详情和答案>>
查看习题详情和答案>>
已知四边形ABCD为菱形,AB=6,∠BAD=60°,两个正三棱锥P-ABD、S-BCD(底面是正三角形且顶点在底面上的射影是底面正三角形的中心)的侧棱长都相等,如图,E、M、N分别在AD、
AB、AP上,且 .
.
(Ⅰ)求证:PB⊥平面PAD;
(Ⅱ)求平面BPS与底面ABCD所成锐二面角的平面角的正切
值;
(Ⅲ)求多面体SPABC的体积.
 查看习题详情和答案>>
查看习题详情和答案>>
AB、AP上,且
 .
.(Ⅰ)求证:PB⊥平面PAD;
(Ⅱ)求平面BPS与底面ABCD所成锐二面角的平面角的正切
值;
(Ⅲ)求多面体SPABC的体积.
 查看习题详情和答案>>
查看习题详情和答案>>
已知四棱锥V—ABCD的顶点V到底面各边所在直线的距离相等,V在底面的射影在四边形ABCD内,在下列各结论中正确的为( )
A.四边形ABCD有外接圆
B.四边形ABCD有内切圆,但顶点V在底面上的射影并不是内切圆的圆心
C.顶点V在底面上的射影是四边形ABCD的内切圆的圆心
D.以上都不对
查看习题详情和答案>>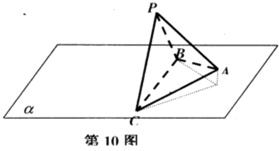 我们把底面是正三角形,顶点在底面的射影是正三角形中心的三棱锥称为正三棱锥、现有一正三棱锥P-ABC放置在平面α上,已知它的底面边长为2,高h,边BC在平面上转动,若某个时刻它在平面α上的射影是等腰直角三角形,则h的取值范围是( )
我们把底面是正三角形,顶点在底面的射影是正三角形中心的三棱锥称为正三棱锥、现有一正三棱锥P-ABC放置在平面α上,已知它的底面边长为2,高h,边BC在平面上转动,若某个时刻它在平面α上的射影是等腰直角三角形,则h的取值范围是( )A、(0,
| ||||||||
B、(0,
| ||||||||
C、(0,
| ||||||||
D、(0,
|