题目内容
已知四边形ABCD为菱形,AB=6,∠BAD=60°,两个正三棱锥P-ABD、S-BCD(底面是正三角形且顶点在底面上的射影是底面正三角形的中心)的侧棱长都相等,如图,E、M、N分别在AD、AB、AP上,且
 .
.(Ⅰ)求证:PB⊥平面PAD;
(Ⅱ)求平面BPS与底面ABCD所成锐二面角的平面角的正切
值;
(Ⅲ)求多面体SPABC的体积.

【答案】分析:(I)取AD中点O,连PO,BO,由等腰三角形三线可一,可得PO⊥AD,BO⊥AD,进而根据线面垂直的判定和性质可得AD⊥PB,由平行线分线段成比例定理,可证得MN∥PB,结合MN⊥PE得PB⊥PE,进而根据线面垂直的判定定理得到PB⊥平面PAD;
(Ⅱ)设P,S在底面的射影分别为P1,S1,取PS中点K,连接BK,DK,由线面夹角的定义,可得∠KBD即可为平面BPS与底面ABCD所成锐二面角的平面角,解三角形即可得到平面BPS与底面ABCD所成锐二面角的平面角.
(III)设P,S在△ABD和△BDC上的射影为H1,H2,根据PS∥AC,可得B-ACSP为四棱锥,分别计算四棱锥底面面积和高,代入即可得到多面体SPABC的体积.
解答: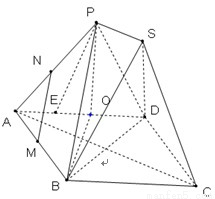 证明:(Ⅰ)取AD中点O,连PO,BO,则PO⊥AD,BO⊥AD
证明:(Ⅰ)取AD中点O,连PO,BO,则PO⊥AD,BO⊥AD
AD⊥平面PBO,
∴AD⊥PB(2分)
又 AN= AP,AM=
AP,AM= AB
AB
∴MN∥PB
∵MN⊥PE
∴PB⊥PE
∵PE∩AD=E
∴PB⊥平面PAD(3分)
解:(Ⅱ)设P,S在底面的射影分别为P1,S1,则
由所给的三棱锥均为正三棱锥且两三棱锥全等,
故PP1∥SS1,且PP1=SS1,∴四边形PSS1P1为平行四边形,
∴PS∥S1P1,又P1,S1分别为△ABD,△BCD的中心,
∴P1,S1在菱形的对角线AC上,
∴PS∥AC,即PS∥平面ABCD…(5分)
设平面PSB与平面ABCD的交线为l,取PS中点K,连接BK,DK,
由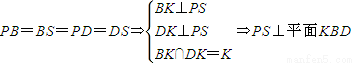
∴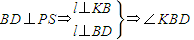 为平面PSB与平面ABCD所成二面角的平面角…(7分)
为平面PSB与平面ABCD所成二面角的平面角…(7分)
在Rt△PP1A中, ,
,
∴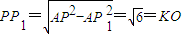 ,
,
∴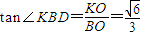 …(9分)
…(9分)
(III)设P,S在△ABD和△BDC上的射影为H1,H2,则H1,H2在直线AC上且PH1∥SH2,且PH1=SH2,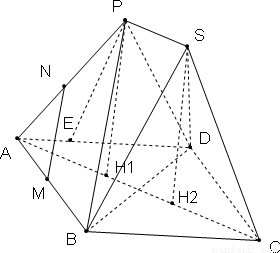
∴则H1H2SP为平行四边形,
∴PS∥AC
∴B-ACSP为四棱锥…7分
设PB=a,则PO2=a2-9,又BO=3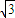 ,由(1)知∠BPO=90°
,由(1)知∠BPO=90°
∴a2+a2-9=(3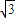 )2,
)2,
∴a2=18,即PB=3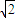
∵PH1⊥平面ABD,
∴PH1⊥BD,
又BD⊥AC
∴BD⊥平面ACSP
设AC∩BD=F
∵四棱锥B-ACSP的高为BF,且BF=3…(9分)
∵H1F= AF,H2F=
AF,H2F= CF,
CF,
∴H1H2= AC=2
AC=2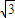 ,
,
∴PS=2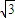 ,
,
在Rt△PH1A中,
PH1=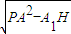 =
=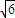
∴SACSP=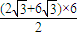 =12
=12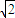
∴多面体SPABC的体积V= •12
•12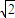 •3=12
•3=12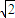
点评:本题考查的知识点是二面角的平面角及求法,直线与平面垂直的判定,其中(I)的关键是证得AD⊥PB,PB⊥PE,(II)的关键是证得∠KBD即可为平面BPS与底面ABCD所成锐二面角的平面角,(III)的关键是证得B-ACSP为四棱锥.
(Ⅱ)设P,S在底面的射影分别为P1,S1,取PS中点K,连接BK,DK,由线面夹角的定义,可得∠KBD即可为平面BPS与底面ABCD所成锐二面角的平面角,解三角形即可得到平面BPS与底面ABCD所成锐二面角的平面角.
(III)设P,S在△ABD和△BDC上的射影为H1,H2,根据PS∥AC,可得B-ACSP为四棱锥,分别计算四棱锥底面面积和高,代入即可得到多面体SPABC的体积.
解答:
 证明:(Ⅰ)取AD中点O,连PO,BO,则PO⊥AD,BO⊥AD
证明:(Ⅰ)取AD中点O,连PO,BO,则PO⊥AD,BO⊥ADAD⊥平面PBO,
∴AD⊥PB(2分)
又 AN=
 AP,AM=
AP,AM= AB
AB∴MN∥PB
∵MN⊥PE
∴PB⊥PE
∵PE∩AD=E
∴PB⊥平面PAD(3分)
解:(Ⅱ)设P,S在底面的射影分别为P1,S1,则
由所给的三棱锥均为正三棱锥且两三棱锥全等,
故PP1∥SS1,且PP1=SS1,∴四边形PSS1P1为平行四边形,
∴PS∥S1P1,又P1,S1分别为△ABD,△BCD的中心,
∴P1,S1在菱形的对角线AC上,
∴PS∥AC,即PS∥平面ABCD…(5分)
设平面PSB与平面ABCD的交线为l,取PS中点K,连接BK,DK,
由
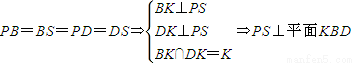
∴
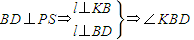 为平面PSB与平面ABCD所成二面角的平面角…(7分)
为平面PSB与平面ABCD所成二面角的平面角…(7分)在Rt△PP1A中,
 ,
,∴
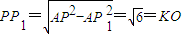 ,
,∴
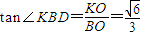 …(9分)
…(9分)(III)设P,S在△ABD和△BDC上的射影为H1,H2,则H1,H2在直线AC上且PH1∥SH2,且PH1=SH2,

∴则H1H2SP为平行四边形,
∴PS∥AC
∴B-ACSP为四棱锥…7分
设PB=a,则PO2=a2-9,又BO=3
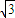 ,由(1)知∠BPO=90°
,由(1)知∠BPO=90°∴a2+a2-9=(3
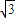 )2,
)2,∴a2=18,即PB=3
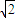
∵PH1⊥平面ABD,
∴PH1⊥BD,
又BD⊥AC
∴BD⊥平面ACSP
设AC∩BD=F
∵四棱锥B-ACSP的高为BF,且BF=3…(9分)
∵H1F=
 AF,H2F=
AF,H2F= CF,
CF,∴H1H2=
 AC=2
AC=2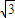 ,
,∴PS=2
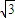 ,
,在Rt△PH1A中,
PH1=
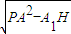 =
=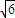
∴SACSP=
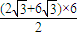 =12
=12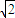
∴多面体SPABC的体积V=
 •12
•12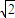 •3=12
•3=12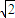
点评:本题考查的知识点是二面角的平面角及求法,直线与平面垂直的判定,其中(I)的关键是证得AD⊥PB,PB⊥PE,(II)的关键是证得∠KBD即可为平面BPS与底面ABCD所成锐二面角的平面角,(III)的关键是证得B-ACSP为四棱锥.

练习册系列答案
相关题目
 如图,已知四边形ABCD为矩形,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE.
如图,已知四边形ABCD为矩形,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE.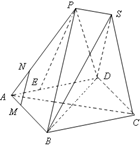 已知四边形ABCD为菱形,AB=6,∠BAD=60°,两个正三棱锥P-ABD、S-BCD(底面是正三角形且顶点在底面上的射影是底面正三角形的中心)的侧棱长都相等,如图,E、M、N分别在AD、
已知四边形ABCD为菱形,AB=6,∠BAD=60°,两个正三棱锥P-ABD、S-BCD(底面是正三角形且顶点在底面上的射影是底面正三角形的中心)的侧棱长都相等,如图,E、M、N分别在AD、 如图,已知四边形ABCD为直角梯形,∠ABC=90°,AD∥BC,AD=2,AB=BC=1,沿AC将△ABC折起,使点B到点P的位置,且平面PAC⊥平面ACD.
如图,已知四边形ABCD为直角梯形,∠ABC=90°,AD∥BC,AD=2,AB=BC=1,沿AC将△ABC折起,使点B到点P的位置,且平面PAC⊥平面ACD. 已知四边形ABCD为直角梯形,∠ADC=90°,AD∥BC,△ABD为等腰直角三角形,平面PAD⊥平面ABCD,E为PA的中点,AD=2BC=
已知四边形ABCD为直角梯形,∠ADC=90°,AD∥BC,△ABD为等腰直角三角形,平面PAD⊥平面ABCD,E为PA的中点,AD=2BC=