摘要：∴ B1E∥AA1.而E是BB1的中点.∴ B1E =.∴ DF∥B1E 且 DF = B1E.∴ 四边形DEB1F是平行四边形.从而 DE∥B1F.注意到 B1F 在平面A1B1C1内.所以 DE∥平面A1B1C1．------------------------------6分(Ⅱ)假设存在点E使平面EAC1⊥平面ACC1A1.则过E作EM⊥AC1于M.过B作BN⊥AC于N.连结MN．∵ 二面角E?AC1?C是直二面角.即平面EAC1⊥ACC1A.∴ EM⊥平面ACC1A．同理可证 BN⊥平面ACC1A．∴ EM∥BN．---8分由B1B∥平面ACC1A1.得 EM = BN.
网址：http://m.1010jiajiao.com/timu_id_34888[举报]
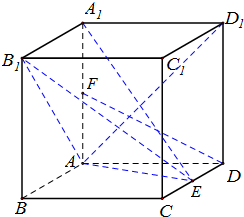（2013•顺义区二模）如图，在长方体ABCD-A1B1C1D1中，AA1=AD=1，E为CD的中点，F为AA1的中点．（I）求证：AD1⊥平面A1B1E；
（II）求证：DF∥平面AB1E；
（III）若二面角A-B1E-A1的大小为45°，求AB的长．
在长方体ABCD-A1B1C1D1中，AA1=AD=2，E是棱CD上的一点．（1）求证：AD1⊥平面A1B1D；
（2）求证：B1E⊥AD1；
（3）若E是棱CD的中点，在棱AA1上是否存在点P，使得DP∥平面B1AE？若存在，求出线段AP的长；若不存在，请说明理由．
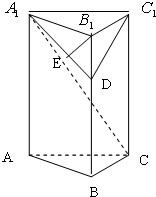如图，在直三棱柱ABC-A1B1C1中，AA1=2，AB=1，∠ABC=90°；点D、E分别在BB1，A1D上，且B1E⊥A1D，四棱锥C-ABDA1与直三棱柱的体积之比为3：5．（1）求异面直线DE与B1C1的距离；
（2）若BC=
| 2 |
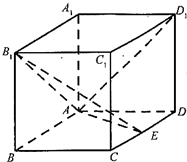（2012•福建）如图，在长方体ABCD-A1B1C1D1中AA1=AD=1，E为CD中点．
在长方体ABCD-A1B1C1D1中，AA1=AD=2，点E在棱CD上，且