Question

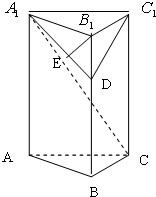如图，在直三棱柱ABC-A₁B₁C₁中，AA₁=2，AB=1，∠ABC=90°；点D、E分别在BB₁，A₁D上，且B₁E⊥A₁D，四棱锥C-ABDA₁与直三棱柱的体积之比为3：5．
（1）求异面直线DE与B₁C₁的距离；
（2）若BC=

2

，求二面角A₁-DC₁-B₁的平面角的正切值．

Answer 1

分析：（1）因B₁C₁⊥A₁B₁，且B₁C₁⊥BB₁，进而可推断B₁C₁⊥面A₁ABB₁，进而推断B₁E是异面直线B₁C₁与DE的公垂线，设BD的长度为x，则四棱椎C-ABDA₁的体积V₁为，里用体积公式表示出V₁，表示出四棱椎C-ABDA₁的体积V₁，同时直三棱柱ABC-A₁B₁C₁的体积V₂，根据V₁：V₂=3：5求得x，从而求得B₁D，直角三角形A₁B₁D中利用勾股定理求得A₁D进而利用三角形面积公式求得B₁E．
（2）过B₁作B₁F⊥C₁D，垂足为F，连接A₁F，因A₁B₁⊥B₁C₁，A₁B₁⊥B₁D，故A₁B₁⊥面B₁DC₁．由三垂线定理知C₁D⊥A₁F，故∠A₁FB₁为所求二面角的平面角，先利用勾股定理求得C₁₁D，进而求得BF，进而可求tan求得∠A₁FB₁．

解答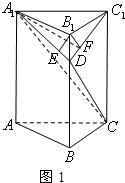：解：（Ⅰ）因B₁C₁⊥A₁B₁，且B₁C₁⊥BB₁，故B₁C₁⊥面A₁ABB₁，
从而B₁C₁⊥B₁E，又B₁E⊥DE，故B₁E是异面直线B₁C₁与DE的公垂线
设BD的长度为x，则四棱椎C-ABDA₁的体积V₁为V1=

1

3

SABDA1?BC=

1

6

(DB+A1A)?AB?BC=

1

6

(x+2)?BC
而直三棱柱ABC-A₁B₁C₁的体积V₂为V2=S△ABC?AA1=

1

2

AB?BC?AA1=BC
由已知条件V₁：V₂=3：5，故

1

6

(x+2)=

3

5

，解之得x=

8

5

从而B1D=B1B-DB=2-

8

5

=

2

5

在直角三角形A₁B₁D中，A1D=

A1B12+B1D2

=

1+( 2 5 )2

=

29

5

，
又因S△A1B1D=

1

2

A1D•B1E=

1

2

A1B1•B1D，
故B1E=

A1B1•B1D

A1D

=

2 29

29

（Ⅱ）如图1，过B₁作B₁F⊥C₁D，垂足为F，连接A₁F，因A₁B₁⊥B₁C₁，A₁B₁⊥B₁D，故A₁B₁⊥面B₁DC₁．
由三垂线定理知C₁D⊥A₁F，故∠A₁FB₁为所求二面角的平面角
在直角△C₁B₁D中，C1D=

B1C12+B1D2

=

2+( 2 5 )2

=

3 6

5

，
又因S△C1B1D=

1

2

C1D•B1F=

1

2

B1C1•B1D，
故B1F=

B1C1•B1D

C1D

=

2 3

9

，所以tanA1FB1=

A1B1

B1F

=

3 3

2

．

点评：本题主要考查了点线面间的距离计算．考查了学生综合分析问题和解决问题的能力．