网址:http://m.1010jiajiao.com/timu_id_346120[举报]
一、填空题:本大题共14小题,每小题5分,计70分.
1. /江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image322.gif) 2.
2. /江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image324.gif) 3.
3./江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image326.gif) 4.
4. /江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image328.gif) 5.68 6. 4 7. 7 8.
5.68 6. 4 7. 7 8. /江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image330.gif)
9./江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image332.gif) 10. 若点P在两渐近线上的射影分别为
10. 若点P在两渐近线上的射影分别为/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image070.gif) 、
、/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image072.gif) ,则
,则/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image074.gif) 必为定值
必为定值/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image337.gif)
11.②③
12./江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image339.gif) 13.1 14.
13.1 14./江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image341.gif)
二、解答题:本大题共6小题,计90分.
15. 解: (Ⅰ)因为/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image156.gif) ,∴
,∴/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image344.gif) ,则
,则/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image346.gif) …………………………………………(4分)
…………………………………………(4分)
∴/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image348.gif) ……………………………………………………………………………(7分)
……………………………………………………………………………(7分)
(Ⅱ)由/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image164.gif) ,得
,得/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image351.gif) ,∴
,∴/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image353.gif) …………………………………………(9分)
…………………………………………(9分)
则/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image355.gif) …………………………………………(11分)
…………………………………………(11分)
由正弦定理,得/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image357.gif) ,∴
,∴/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image154.gif) 的面积为
的面积为/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image359.gif) ………………………(14分)
………………………(14分)
16. (Ⅰ)解:因为/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image190.gif) ,
,/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image361.gif) ,且
,且/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image363.gif) ,
,
所以/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image365.gif) ……………………………………………………………………………………………(4分)
……………………………………………………………………………………………(4分)
又/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image180.gif) ,所以四边形
,所以四边形/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image367.gif) 为平行四边形,则
为平行四边形,则/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image369.gif) ……………………………………(6分)
……………………………………(6分)
而/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image184.gif) ,故点
,故点/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image186.gif) 的位置满足
的位置满足/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image371.gif) ………………………………………………………(7分)
………………………………………………………(7分)
(Ⅱ)证: 因为侧面/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image173.gif) 底面
底面/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image175.gif) ,
,/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image373.gif) ,且
,且/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image375.gif) ,
,
所以/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image377.gif) ,则
,则/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image379.gif) …………………………………………………………………(10分)
…………………………………………………………………(10分)
又/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image177.gif) ,且
,且/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image381.gif) ,所以
,所以/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image383.gif) …………(13分)
…………(13分)
而/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image385.gif) ,所以
,所以/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image192.gif) …………………………………………………(14分)
…………………………………………………(14分)
17. 解:(Ⅰ)因为/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image387.gif) ,所以
,所以/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image197.gif) 的面积为
的面积为/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image389.gif) (
(/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image391.gif) )………………………(2分)
)………………………(2分)
设正方形/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image206.gif) 的边长为
的边长为/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image152.gif) ,则由
,则由/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image394.gif) ,得
,得/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image396.gif) ,
,
解得/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image398.gif) ,则
,则/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image400.gif) …………………………………………………………………(6分)
…………………………………………………………………(6分)
所以/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image402.gif) ,则
,则/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image404.gif) ………………(9分)
………………(9分)
(Ⅱ)因为/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image406.gif) ,所以
,所以/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image408.gif)
/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image410.gif) ……………(13分)
……………(13分)
当且仅当/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image412.gif) 时取等号,此时
时取等号,此时/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image414.gif) .所以当
.所以当/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image219.gif) 长为
长为/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image417.gif) 时,
时,/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image068.gif) 有最小值1…………………(15分)
有最小值1…………………(15分)
18. 解:(Ⅰ)设圆心/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image051.gif)
/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image419.gif) ,则
,则/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image421.gif) ,解得
,解得/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image423.gif) …………………………………(3分)
…………………………………(3分)
则圆/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image051.gif) 的方程为
的方程为/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image425.gif) ,将点
,将点/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image008.gif) 的坐标代入得
的坐标代入得/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image428.gif) ,故圆
,故圆/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image051.gif) 的方程为
的方程为/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image430.gif) ………(5分)
………(5分)
(Ⅱ)设/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image432.gif) ,则
,则/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image430.gif) ,且
,且/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image434.gif) …………………………(7分)
…………………………(7分)
=/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image436.gif) =
=/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image438.gif) ,所以
,所以/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image233.gif) 的最小值为
的最小值为/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image440.gif) (可由线性规划或三角代换求得)…(10分)
(可由线性规划或三角代换求得)…(10分)
(Ⅲ)由题意知, 直线/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image111.gif) 和直线
和直线/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image120.gif) 的斜率存在,且互为相反数,故可设
的斜率存在,且互为相反数,故可设/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image442.gif) ,
,
/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image444.gif) ,由
,由/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image446.gif) ,得
,得/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image448.gif) ………(11分)
………(11分)
因为点/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image008.gif) 的横坐标
的横坐标/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image451.gif) 一定是该方程的解,故可得
一定是该方程的解,故可得/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image453.gif) ………………………………(13分)
………………………………(13分)
同理,/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image455.gif) ,所以
,所以/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image457.gif) =
=/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image459.gif)
所以,直线/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image199.gif) 和
和/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image241.gif) 一定平行…………………………………………………………………………(15分)
一定平行…………………………………………………………………………(15分)
19. (Ⅰ)解:因为/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image461.gif) …………………………………(2分)
…………………………………(2分)
由/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image463.gif) ;由
;由/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image465.gif) ,所以
,所以/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image253.gif) 在
在/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image468.gif) 上递增,
上递增,
在/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image470.gif) 上递减 …………………………………………………………………………………………(4分)
上递减 …………………………………………………………………………………………(4分)
欲/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image253.gif) 在
在/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image246.gif) 上为单调函数,则
上为单调函数,则/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image472.gif) ………………………………………………………(5分)
………………………………………………………(5分)
(Ⅱ)证:因为/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image253.gif) 在
在/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image468.gif) 上递增,在
上递增,在/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image470.gif) 上递减,所以
上递减,所以/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image253.gif) 在
在/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image451.gif) 处取得极小值
处取得极小值/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image475.gif) (7分)
(7分)
又/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image477.gif) ,所以
,所以/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image253.gif) 在
在/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image479.gif) 上的最小值为
上的最小值为/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image481.gif) …………………………………(9分)
…………………………………(9分)
从而当/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image248.gif) 时,
时,/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image484.gif) ,即
,即/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image486.gif) …………………………………………………………(10分)
…………………………………………………………(10分)
(Ⅲ)证:因为/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image488.gif) ,所以
,所以/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image261.gif) 即为
即为/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image490.gif) ,
,
令/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image492.gif) ,从而问题转化为证明方程
,从而问题转化为证明方程/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image492.gif) =0
=0
在/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image494.gif) 上有解,并讨论解的个数……………………………………………………………………(12分)
上有解,并讨论解的个数……………………………………………………………………(12分)
因为/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image496.gif) ,
,/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image498.gif) ,所以
,所以
①当/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image500.gif) 时,
时,/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image502.gif) ,所以
,所以/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image504.gif) 在
在/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image494.gif) 上有解,且只有一解 ……(13分)
上有解,且只有一解 ……(13分)
②当/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image507.gif) 时,
时,/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image509.gif) ,但由于
,但由于/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image511.gif) ,
,
所以/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image504.gif) 在
在/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image494.gif) 上有解,且有两解 …………………………………………………………(14分)
上有解,且有两解 …………………………………………………………(14分)
③当/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image514.gif) 时,
时,/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image516.gif) ,所以
,所以/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image504.gif) 在
在/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image494.gif) 上有且只有一解;
上有且只有一解;
当/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image519.gif) 时,
时,/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image521.gif) ,
,
所以/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image504.gif) 在
在/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image523.gif) 上也有且只有一解…………………………………………………………(15分)
上也有且只有一解…………………………………………………………(15分)
综上所述, 对于任意的/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image257.gif) ,总存在
,总存在/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image259.gif) ,满足
,满足/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image261.gif) ,
,
且当/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image525.gif) 时,有唯一的
时,有唯一的/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image037.gif) 适合题意;当
适合题意;当/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image507.gif) 时,有两个
时,有两个/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image037.gif) 适合题意…………(16分)
适合题意…………(16分)
(说明:第(Ⅱ)题也可以令/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image528.gif) ,
,/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image530.gif) ,然后分情况证明
,然后分情况证明/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image532.gif) 在其值域内,并讨论直线
在其值域内,并讨论直线/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image534.gif) 与函数
与函数/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image536.gif) 的图象的交点个数即可得到相应的
的图象的交点个数即可得到相应的/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image037.gif) 的个数)
的个数)
20.(Ⅰ)解:由题意得,/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image538.gif) ,所以
,所以/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image268.gif) =
=/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image541.gif) ……………………(4分)
……………………(4分)
(Ⅱ)证:令/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image543.gif) ,
,/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image545.gif) ,则
,则/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image135.gif) =1………………………………………………(5分)
=1………………………………………………(5分)
所以/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image266.gif) =
=/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image547.gif) (1),
(1),/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image549.gif) =
=/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image551.gif) (2),
(2),
(2)―(1),得/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image553.gif) ―
―/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image555.gif) =
=/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image557.gif) ,
,
化简得/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image559.gif) (3)……………………………………………………………(7分)
(3)……………………………………………………………(7分)
/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image561.gif) (4),(4)―(3)得
(4),(4)―(3)得/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image563.gif) …………(9分)
…………(9分)
在(3)中令/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image543.gif) ,得
,得/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image565.gif) ,从而
,从而/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image055.gif) 为等差数列 …………………………………………(10分)
为等差数列 …………………………………………(10分)
(Ⅲ)记/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image567.gif) ,公差为
,公差为/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image306.gif) ,则
,则/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image278.gif) =
=/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image570.gif) …………………(12分)
…………………(12分)
则/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image572.gif) ,
,/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image574.gif)
/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image576.gif)
/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image578.gif) …………………………………………(14分)
…………………………………………(14分)
则/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image580.gif) ,当且仅当
,当且仅当/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image582.gif) ,即
,即/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image584.gif) 时等号成立……………(16分)
时等号成立……………(16分)
数学附加题部分
21.A.(几何证明选讲选做题)
解:因为PB=PD+BD=1+8=9,/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image586.gif) =PD?BD=9,PA=3,AE=PA=3,连结AD,在
=PD?BD=9,PA=3,AE=PA=3,连结AD,在/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image588.gif) 中,得
中,得/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image590.gif) ……(5分)
……(5分)
又/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image592.gif) ,所以
,所以/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image594.gif) …………………………………………………………………(10分)
…………………………………………………………………(10分)
B.(矩阵与变换选做题)
解: (Ⅰ)设/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image596.gif) ,则有
,则有/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image596.gif)
/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image598.gif) =
=/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image600.gif) ,
,/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image596.gif)
/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image602.gif) =
=/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image604.gif) ,
,
所以/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image606.gif) ,解得
,解得/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image608.gif) …………………………………………………………(4分)
…………………………………………………………(4分)
所以M=/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image610.gif) ,从而
,从而/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image298.gif) =
=/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image612.gif) ………………………………………………………………(7分)
………………………………………………………………(7分)
(Ⅱ)因为/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image614.gif) 且m:2
且m:2/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image616.gif) ,
,
所以2(x+2y)-(3x+4y)=4,即x+4 =0,这就是直线l的方程 ………………………………………(10分)
C.(坐标系与参数方程选做题)
解:将极坐标方程/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image302.gif) 转化为普通方程:
转化为普通方程:/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image619.gif) ……………………………………………(2分)
……………………………………………(2分)
/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image621.gif) 可化为
可化为/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image623.gif) …………………………………………………………(5分)
…………………………………………………………(5分)
在/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image619.gif) 上任取一点A
上任取一点A/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image626.gif) ,则点A到直线的距离为
,则点A到直线的距离为
/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image628.gif) ,它的最大值为4
……………………………(10分)
,它的最大值为4
……………………………(10分)
D.(不等式选讲选做题)
证:左=/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image630.gif)
/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image632.gif) …(5分)
…(5分)
/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image634.gif)
/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image636.gif) ……………………(10分)
……………………(10分)
22.解:以OA、OB所在直线分别x轴,y轴,以过O且垂直平面ABCD的直线为z轴,建立空间直角坐标系,则/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image638.gif) ,
,/江苏省盐城市2008-2009高三第一次调研考试数学试题.files/image640.gif) …(2分)
…(2分)
(Ⅰ)设平面PDB的法向量为
(12分)若![]() ,
,![]() ,其中
,其中![]() ,函数
,函数![]() ,且
,且![]() 的图象关于直线
的图象关于直线![]() 对称.
对称.
(1)求![]() 的解析式及
的解析式及![]() 的单调区间;
的单调区间;
(2)将![]() 的图象向左平移
的图象向左平移![]() 个单位,再将得到的图象的横坐标变为原来的2倍(纵坐标不变)后得到的
个单位,再将得到的图象的横坐标变为原来的2倍(纵坐标不变)后得到的![]() 的图象;若函数
的图象;若函数![]() ,
,![]() 的图象与
的图象与![]() 的图象有三个交点且交点的横坐标成等比数列,求
的图象有三个交点且交点的横坐标成等比数列,求![]() 的值.
的值.
若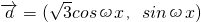 ,
,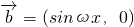 ,其中
,其中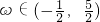 ,函数
,函数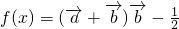 ,且f(x)的图象关于直线
,且f(x)的图象关于直线 对称.
对称.
(1)求f(x)的解析式及f(x)的单调区间;
(2)将y=f(x)的图象向左平移 个单位,再将得到的图象的横坐标变为原来的2倍(纵坐标不变)后得到的y=g(x)的图象;若函数y=g(x),
个单位,再将得到的图象的横坐标变为原来的2倍(纵坐标不变)后得到的y=g(x)的图象;若函数y=g(x),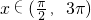 的图象与y=a的图象有三个交点且交点的横坐标成等比数列,求a的值.
的图象与y=a的图象有三个交点且交点的横坐标成等比数列,求a的值.
查看习题详情和答案>>
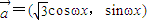 ,
,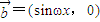 ,其中
,其中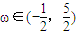 ,函数
,函数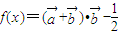 ,且f(x)的图象关于直线
,且f(x)的图象关于直线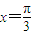 对称.
对称.(1)求f(x)的解析式及f(x)的单调区间;
(2)将y=f(x)的图象向左平移
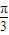 个单位,再将得到的图象的横坐标变为原来的2倍(纵坐标不变)后得到的y=g(x)的图象;若函数y=g(x),
个单位,再将得到的图象的横坐标变为原来的2倍(纵坐标不变)后得到的y=g(x)的图象;若函数y=g(x),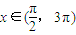 的图象与y=a的图象有三个交点且交点的横坐标成等比数列,求a的值.
的图象与y=a的图象有三个交点且交点的横坐标成等比数列,求a的值.查看习题详情和答案>>

 ,
, ,其中
,其中 ,函数
,函数 ,且f(x)的图象关于直线
,且f(x)的图象关于直线 对称.
对称. 个单位,再将得到的图象的横坐标变为原来的2倍(纵坐标不变)后得到的y=g(x)的图象;若函数y=g(x),
个单位,再将得到的图象的横坐标变为原来的2倍(纵坐标不变)后得到的y=g(x)的图象;若函数y=g(x), 的图象与y=a的图象有三个交点且交点的横坐标成等比数列,求a的值.
的图象与y=a的图象有三个交点且交点的横坐标成等比数列,求a的值.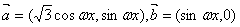 ,其中
,其中 ,函数
,函数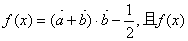 的图象关于直线
的图象关于直线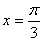 对称.
对称.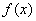 的解析式;
的解析式;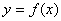 的图象向左平移
的图象向左平移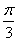 个单位,再将得到的图象的横坐标变为原来的2倍(纵坐标不变)后得到
个单位,再将得到的图象的横坐标变为原来的2倍(纵坐标不变)后得到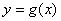 的图象;若函数
的图象;若函数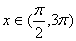 的图象与
的图象与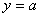 的图象有三个交点且交点的横坐标成等比数列,求
的图象有三个交点且交点的横坐标成等比数列,求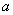 的值.
的值.