摘要：16．解:命题: -------------------------------3分
网址：http://m.1010jiajiao.com/timu_id_340346[举报]
命题：
①设
、
、
是互不共线的非零向量，则（
•
）
-（
•
）
=
；
②“a=1”是“函数f（x）=lg（ax+1）在（0，+∞）单调递增”的充分不必要条件；
③已知α，β∈R，则“α=β”是“tanα=tanβ”的充要条件；
④函数f（x）=2x-x2的在（1，3）上至少一个零点；
⑤
(x-2)≥0的解集为[2，+∞）；
⑥函数y=x3在x=0处切线不存在．
其中正确命题的个数为（ ）
①设
| a |
| b |
| c |
| a |
| b |
| c |
| c |
| a |
| b |
| 0 |
②“a=1”是“函数f（x）=lg（ax+1）在（0，+∞）单调递增”的充分不必要条件；
③已知α，β∈R，则“α=β”是“tanα=tanβ”的充要条件；
④函数f（x）=2x-x2的在（1，3）上至少一个零点；
⑤
| x-1 |
⑥函数y=x3在x=0处切线不存在．
其中正确命题的个数为（ ）
查看习题详情和答案>>
命题：
①设
、
、
是互不共线的非零向量，则（
•
）
-（
•
）
=
；
②“a=1”是“函数f（x）=lg（ax+1）在（0，+∞）单调递增”的充分不必要条件；
③已知α，β∈R，则“α=β”是“tanα=tanβ”的充要条件；
④函数f（x）=2x-x2的在（1，3）上至少一个零点；
⑤
(x-2)≥0的解集为[2，+∞）；
⑥函数y=x3在x=0处切线不存在．
其中正确命题的个数为（ ）
查看习题详情和答案>>
①设
| a |
| b |
| c |
| a |
| b |
| c |
| c |
| a |
| b |
| 0 |
②“a=1”是“函数f（x）=lg（ax+1）在（0，+∞）单调递增”的充分不必要条件；
③已知α，β∈R，则“α=β”是“tanα=tanβ”的充要条件；
④函数f（x）=2x-x2的在（1，3）上至少一个零点；
⑤
| x-1 |
⑥函数y=x3在x=0处切线不存在．
其中正确命题的个数为（ ）
| A．1 | B．2 | C．3 | D．4 |
命题：
①设
、
、
是互不共线的非零向量，则
-
=
；
②“a=1”是“函数f（x）=lg（ax+1）在（0，+∞）单调递增”的充分不必要条件；
③已知α，β∈R，则“α=β”是“tanα=tanβ”的充要条件；
④函数f（x）=2x-x2的在（1，3）上至少一个零点；
⑤
的解集为[2，+∞）；
⑥函数y=x3在x=0处切线不存在．
其中正确命题的个数为（ ）
A．1
B．2
C．3
D．4
查看习题详情和答案>>
①设
、、是互不共线的非零向量，则-=；②“a=1”是“函数f（x）=lg（ax+1）在（0，+∞）单调递增”的充分不必要条件；
③已知α，β∈R，则“α=β”是“tanα=tanβ”的充要条件；
④函数f（x）=2x-x2的在（1，3）上至少一个零点；
⑤
的解集为[2，+∞）；⑥函数y=x3在x=0处切线不存在．
其中正确命题的个数为（ ）
A．1
B．2
C．3
D．4
查看习题详情和答案>>
、
、
是互不共线的非零向量，则（
；
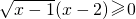的解集为[2，+∞）；