摘要:解:(Ⅰ)∵DE⊥平面ACD.AF平面ACD ∴DE⊥AF
网址:http://m.1010jiajiao.com/timu_id_33612[举报]
 (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分)A.(不等式选做题).不等式:|x-1|+|x+2|<5的解集是
{x|-3<x<2}
{x|-3<x<2}
.B.(几何证明选做题)如图,在△ABC中,DE∥BC,EF∥CD,若BC=3,DE=2,DF=1,则AB的长为
| 9 |
| 2 |
| 9 |
| 2 |
C.(坐标系与参数方程选做题)在已知极坐标系中,已知圆ρ=2cosθ与直线 3ρcosθ+4ρsinθ+a=0相切,则实数a=
2或8
2或8
. A.(不等式选做题)不等式|
A.(不等式选做题)不等式|| x+2 |
| x+1 |
B.(几何证明选做题)如图,在△ABC中,AB=AC,以BC为直径的半圆O与边AB相交于点D,切线DE⊥AC,垂足为点E.则
| AE |
| CE |
C.(坐标系与参数方程选做题)若△ABC的底边BC=10,∠B=2∠A,以B点为极点,BC 为极轴,则顶点A 的极坐标方程为
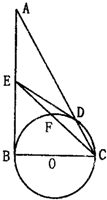 (选修4-1)如图,在△ABC中,∠ABC=90°,以BC为直径的圆O交AC于点D,设E为AB的中点.
(选修4-1)如图,在△ABC中,∠ABC=90°,以BC为直径的圆O交AC于点D,设E为AB的中点. (I)求证:直线DE为圆O的切线;
(Ⅱ)设CE交圆O于点F,求证:CD•CA=CF•CE
(选修4-4)在平面直角坐标系xoy中,圆C的参数方程为
|
| π |
| 3 |
(I)写出圆C的标准方程和直线l的参数方程;
(Ⅱ)设直线l与圆C相交于A,B两点,求|PA|-|PB|的值.
(选修4-5)已知函数f(x)=|2x+1|,g(x)=|x|+a
(Ⅰ)当a=0时,解不等式f(x)≥g(x);
(Ⅱ)若存在x∈R,使得f(x)≤g(x)成立,求实数a的取值范围.
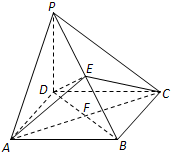 如图,在四棱锥P-ABCD中,PD⊥平面ABCD;四边形ABCD是菱形,边长为2,∠BCD=60°,经过AC作与PD平行的平面交PB与点E,ABCD的两对角线交点为F.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD;四边形ABCD是菱形,边长为2,∠BCD=60°,经过AC作与PD平行的平面交PB与点E,ABCD的两对角线交点为F. (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分.)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分.)