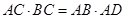题目内容
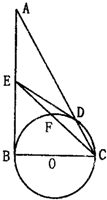 (选修4-1)如图,在△ABC中,∠ABC=90°,以BC为直径的圆O交AC于点D,设E为AB的中点.
(选修4-1)如图,在△ABC中,∠ABC=90°,以BC为直径的圆O交AC于点D,设E为AB的中点. (I)求证:直线DE为圆O的切线;
(Ⅱ)设CE交圆O于点F,求证:CD•CA=CF•CE
(选修4-4)在平面直角坐标系xoy中,圆C的参数方程为
|
| π |
| 3 |
(I)写出圆C的标准方程和直线l的参数方程;
(Ⅱ)设直线l与圆C相交于A,B两点,求|PA|-|PB|的值.
(选修4-5)已知函数f(x)=|2x+1|,g(x)=|x|+a
(Ⅰ)当a=0时,解不等式f(x)≥g(x);
(Ⅱ)若存在x∈R,使得f(x)≤g(x)成立,求实数a的取值范围.
分析:(选修4-1)(Ⅰ)利用条件、等腰三角形的性质求得∠EDO=∠EDB+∠ODB=∠EBD+∠OBD=90°,可得直线DE为圆O的切线.
(Ⅱ)连接DF,则有∠DFC=∠DBC,证明 D、A、E、F四点共圆,可得 CD•CA=CF•CE.
(选修4-4)(Ⅰ)把圆的参数方程利用同角三角函数的基本关系消去参数,化为标准方程.把直线l的参数方程消去参数,化为直角坐标方程.
(Ⅱ)把直线的方程代入圆的方程,利用根与系数的关系以及参数的几何意义求得|PA|•|PB|的值.
(选修4-5)(Ⅰ)当 a=0 时,由f(x)≥g(x) 得|2x+1|≥x,两边平方整理得 3x2+4x+1≥0,解此一元二次不等式求得x的范围,即为所求.
(Ⅱ)由 f(x)≤g(x) 得 a≥|2x+1|-|x|,令h(x)=|2x+1|-|x|,求得 h(x)的最小值,即可求得实数a的取值范围.
(Ⅱ)连接DF,则有∠DFC=∠DBC,证明 D、A、E、F四点共圆,可得 CD•CA=CF•CE.
(选修4-4)(Ⅰ)把圆的参数方程利用同角三角函数的基本关系消去参数,化为标准方程.把直线l的参数方程消去参数,化为直角坐标方程.
(Ⅱ)把直线的方程代入圆的方程,利用根与系数的关系以及参数的几何意义求得|PA|•|PB|的值.
(选修4-5)(Ⅰ)当 a=0 时,由f(x)≥g(x) 得|2x+1|≥x,两边平方整理得 3x2+4x+1≥0,解此一元二次不等式求得x的范围,即为所求.
(Ⅱ)由 f(x)≤g(x) 得 a≥|2x+1|-|x|,令h(x)=|2x+1|-|x|,求得 h(x)的最小值,即可求得实数a的取值范围.
解答:(选修4-1)(Ⅰ)证明:连接BD、OD,在Rt△ABD中,DE=
=BE,则在等腰三角形EBD中,∠EBD=∠EDB.
在等腰三角形OBD中,∠OBD=∠ODB,可得∠EDO=∠EDB+∠ODB=∠EBD+∠OBD=90°,
即直线DE为圆O的切线.

(Ⅱ)连接DF,则有∠DFC=∠DBC,
又因为∠A=∠DBC,可得∠A=∠DFC,则有 D、A、E、F四点共圆.
因此得到CD•CA=CF•CE.
(选修4-4)解:(Ⅰ)圆的标准方程为 x2+y2=16,
直线l的参数方程为
,即
(t为参数).
(Ⅱ)把直线的方程
代入 x2+y2=16,
得 (2+
)2+(2+
)2=16,t2+2(
+1)t-8=0.
所以 t1•t2=-8,即|PA|•|PB|=8.
(选修4-5)解:(Ⅰ)当 a=0 时,由f(x)≥g(x) 得|2x+1|≥x,
两边平方整理得 3x2+4x+1≥0,
解之得x≤-1,或 x≥-
,∴原不等式的解集为(-∞,-1]∪[-
,+∞).
(Ⅱ)由 f(x)≤g(x) 得 a≥|2x+1|-|x|,
令h(x)=|2x+1|-|x|,则 h(x)=
,∴h(x) 的最小值为h(-
)=-
,
从而所求实数 a的范围为[-
,+∞).
| AB |
| 2 |
在等腰三角形OBD中,∠OBD=∠ODB,可得∠EDO=∠EDB+∠ODB=∠EBD+∠OBD=90°,
即直线DE为圆O的切线.

(Ⅱ)连接DF,则有∠DFC=∠DBC,
又因为∠A=∠DBC,可得∠A=∠DFC,则有 D、A、E、F四点共圆.
因此得到CD•CA=CF•CE.
(选修4-4)解:(Ⅰ)圆的标准方程为 x2+y2=16,
直线l的参数方程为
|
|
(Ⅱ)把直线的方程
|
得 (2+
| t |
| 2 |
| ||
| 2 |
| 3 |
所以 t1•t2=-8,即|PA|•|PB|=8.
(选修4-5)解:(Ⅰ)当 a=0 时,由f(x)≥g(x) 得|2x+1|≥x,
两边平方整理得 3x2+4x+1≥0,
解之得x≤-1,或 x≥-
| 1 |
| 3 |
| 1 |
| 3 |
(Ⅱ)由 f(x)≤g(x) 得 a≥|2x+1|-|x|,
令h(x)=|2x+1|-|x|,则 h(x)=
|
| 1 |
| 2 |
| 1 |
| 2 |
从而所求实数 a的范围为[-
| 1 |
| 2 |
点评:本题主要考查圆的参数方程、圆的切线方程、与圆有关的比例线段,绝对值不等式的解法,属于中档题.

练习册系列答案
相关题目
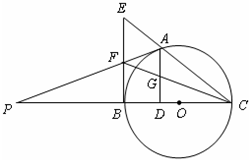 选修4-1:
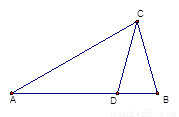
选修4-1: (选修4-1)如图,若△ACD~△ABC,则下列式子中成立的是( )
(选修4-1)如图,若△ACD~△ABC,则下列式子中成立的是( )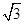 ,PC=1,则圆O的半径为________ .
,PC=1,则圆O的半径为________ .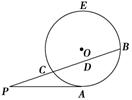
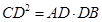 B.
B.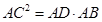
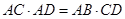 D.
D.