网址:http://m.1010jiajiao.com/timu_id_329242[举报]
一. ADBCA CABBA BC
二.
13.3; 14.(-∞,4]; 15.  ; 16.
; 16.  .
.
三.
17. 解:解:由 ,得
,得 …3分
…3分

 ………………6分
………………6分
又
 =
=  。………10分
。………10分
18. 解:(I)分别记“客人游览甲景点”,“客人游览乙景点”,“客人游览丙景点”为事件A1,A2,A3.由已知A1,A2,A3相互独立,P(A1)= 0.4,P(A2)= 0.5,P(A3)= 0.6.
P(ξ= 3)= P(A1?A2?A3)+P(A1?A2?A3)
= P(A1)P(A2)P(A3)+P(A1)P(A2)P(A3))
= 2×0.4×0.5×0.6=
(Ⅱ)客人游览的景点数的可能取值为0,1,2,3.相应地,客人没有游览的景点数的可能取值为3,2,1,0,所以ξ的可能取值为1,3.∴P(ξ= 1)= 1-0.24= 0.76. ………12分
19、解:解法一:(Ⅰ)取 中点
中点 ,连结
,连结 .
.
 为正三角形,
为正三角形, .
.
 正三棱柱
正三棱柱 中,平面
中,平面 平面
平面 ,
,

 平面
平面 .
.
连结 ,在正方形
,在正方形 中,
中, 分别为
分别为
 的中点,
的中点,
 ,
,
 .………………………………….3分
.………………………………….3分
在正方形 中,
中, ,
,
 平面
平面 .………………………………….5分
.………………………………….5分
(Ⅱ)设 与
与 交于点
交于点 ,在平面
,在平面 中,作
中,作 于
于 ,连结
,连结 ,由(Ⅰ)得
,由(Ⅰ)得 平面
平面 .
.
 ,
,
 为二面角
为二面角 的平面角.………………………………….9分
的平面角.………………………………….9分
在 中,由等面积法可求得
中,由等面积法可求得 ,
,
又 ,
,
 .
.
所以二面角 的正弦值
的正弦值 .………………………………….12分
.………………………………….12分
解法二:(Ⅰ)取 中点
中点 ,连结
,连结 .
.
 为正三角形,
为正三角形, .$
.$
 平面
平面 .
.
取 中点
中点 ,以
,以 为原点,
为原点, ,
, ,
, 的方向为
的方向为 轴的正方向建立空间直角坐标系,则
轴的正方向建立空间直角坐标系,则 ,
, ,
, ,
, ,
, …….3分
…….3分
 ,
, ,
, .
.
 ,
, ,
,

 ,
, .
.
 平面
平面 .………………………………….6分
.………………………………….6分
(Ⅱ)设平面 的法向量为
的法向量为 .
.
 ,
, .
.
 ,
, ,
,



令 得
得 为平面
为平面 的一个法向量.…………………………9分
的一个法向量.…………………………9分
由(Ⅰ)知 平面
平面 ,
,
 为平面
为平面 的法向量.
的法向量.
 ,
, .
.
 二面角
二面角 的正弦值
的正弦值 …………………………12
…………………………12
20.
解:(1)由已知得 解得
解得 .
.
设数列 的公比为
的公比为 ,由
,由 ,可得
,可得 .
.
又 ,可知
,可知 ,
,
即 ,
解得
,
解得 .
.
由题意得 .
. .
故数列
.
故数列 的通项为
的通项为 .…………6
.…………6
(2)由于
由(1)得
 又
又
 是等差数列.
是等差数列.
 =
= =
=
故 .…………………………12
.…………………………12
21.解:解:(Ⅰ)由题意知f′(x)= ax2+bx-a2,且f′(x)= 0的两根为x1、x2.
∴x1+x2= - x1x2= -a.
∴(x2-x1)2= (x2+x1)2-4x1x2= 4.
∴()2+
∴b2= (4-
(Ⅱ)由(1)知b2= (4-
令函数g(a)= (4-
g′(a)=
-
令g'(a)= 0 ∴a1= 0,a2= .
函数g(a)在(0,)上为增函数,(,1)上为减函数.
∴g(a)max= g()= .
∴b2≤.
∴|b|≤.…………………………12分
22.解:(Ⅰ)由双曲线的定义可知,曲线 是以
是以 为焦点的双曲线的左支,且
为焦点的双曲线的左支,且 ,易知
,易知
故曲线 的方程为
的方程为 …………………………3
…………………………3
设 ,由题意建立方程组
,由题意建立方程组
消去 ,得
,得
又已知直线与双曲线左支交于两点 ,有
,有
 解得
解得 ………………5
………………5
∵ 



依题意得 
 整理后得
整理后得
∴ 或
或 但
但 ∴
∴
故直线 的方程为
的方程为 …………………………8
…………………………8
设 ,由已知
,由已知 ,得
,得
∴ ,
,
又 ,
,
∴点
将点 的坐标代入曲线
的坐标代入曲线 的方程,得
的方程,得 得
得 ,
,
但当 时,所得的点在双曲线的右支上,不合题意
时,所得的点在双曲线的右支上,不合题意
∴ .…………………………10
.…………………………10
点 的坐标为
的坐标为
 到
到 的距离为
的距离为
∴ 的面积
的面积 …………………………12
…………………………12



⑴求数列
 的通项公式;
的通项公式;⑵设
 ,若
,若 对
对 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;⑶是否存在以
 为首项,公比为
为首项,公比为 的数列
的数列 ,
, ,使得数列
,使得数列 中每一项都是数列
中每一项都是数列 中不同的项,若存在,求出所有满足条件的数列
中不同的项,若存在,求出所有满足条件的数列 的通项公式;若不存在,说明理由
的通项公式;若不存在,说明理由设数列![]() 的通项公式为
的通项公式为![]() 。数列
。数列![]() 定义如下:对于正整数m,
定义如下:对于正整数m,![]() 是使得不等式
是使得不等式![]() 成立的所有n中的最小值。 (1)若
成立的所有n中的最小值。 (1)若![]() ,求b3; (2)若
,求b3; (2)若![]() ,求数列
,求数列![]() 的前2m项和公式;(3)是否存在p和q,使得
的前2m项和公式;(3)是否存在p和q,使得![]() ?如果存在,求p和q的取值范围;如果不存在,请说明理由。
?如果存在,求p和q的取值范围;如果不存在,请说明理由。
 的通项公式为
的通项公式为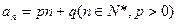 。数列
。数列 定义如下:对于正整数m,
定义如下:对于正整数m, 是使得不等式
是使得不等式 成立的所有n中的最小值。 (1)若
成立的所有n中的最小值。 (1)若 ,求b3; (2)若
,求b3; (2)若 ,求数列
,求数列 的前2m项和公式;(3)是否存在p和q,使得
的前2m项和公式;(3)是否存在p和q,使得 ?如果存在,求p和q的取值范围;如果不存在,请说明理由。
?如果存在,求p和q的取值范围;如果不存在,请说明理由。