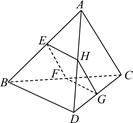
摘要：16．如图.已知AB⊥平面ACD.DE⊥平面ACD.AC=AD.DE＝2AB.F为CD的中点． (1) 求证:AF∥平面BCE, (2) 求证:平面BCE⊥平面CDE． [证明](1)因为AB⊥平面ACD.DE⊥平面ACD. 所以AB∥DE. 取CE的中点G.连结BG.GF.因为F为的中点. 所以GF∥ED∥BA. GF＝ED＝BA. 从而ABGF是平行四边形.于是AF∥BG. --------4分 因为AF平面BCE.BG平面BCE.所以AF∥平面BCE． --------7分 (2)因为AB⊥平面ACD.AF平面ACD. 所以AB⊥AF.即ABGF是矩形.所以AF⊥GF. --------9分 又AC=AD.所以AF⊥CD. ------- 11分 而CD∩GF＝F.所以AF⊥平面GCD.即AF⊥平面CDE. 因为AF∥BG.所以BG⊥平面CDE. 因为BG平面BCE.所以平面BCE⊥平面CDE． ------- 14分

网址：http://m.1010jiajiao.com/timu_id_3206420[举报]