摘要：12．两圆的位置关系的判定方法. 设两圆圆心分别为O1.O2.半径分别为r1.r2.|O1O2|为圆心距.则两圆位置关系如下: |O1O2|>r1+r2两圆外离, |O1O2|=r1+r2两圆外切, | r1-r2|<|O1O2|< r1+r2两圆相交, | O1O2 |=| r1-r2|两圆内切, 0<| O1O2|<| r1-r2|两圆内含.
网址：http://m.1010jiajiao.com/timu_id_3203308[举报]
三题中任选两题作答
（1）（2011年江苏高考）已知矩阵A=
，向量β=
，求向量α，使得A2α=β
（2）（2011年山西六校模考）以直角坐标系的原点O为极点，x轴的正半轴为极轴，已知点P的直角坐标为（1，-5），点M的极坐标为(4，
)，若直线l过点P，且倾斜角为
，圆C以M为圆心、4为半径．
①求直线l的参数方程和圆C的极坐标方程； ②试判定直线l和圆C的位置关系．
（3）若正数a，b，c满足a+b+c=1，求
+
+
的最小值．
查看习题详情和答案>>
（1）（2011年江苏高考）已知矩阵A=
|
|
（2）（2011年山西六校模考）以直角坐标系的原点O为极点，x轴的正半轴为极轴，已知点P的直角坐标为（1，-5），点M的极坐标为(4，
| π |
| 2 |
| π |
| 3 |
①求直线l的参数方程和圆C的极坐标方程； ②试判定直线l和圆C的位置关系．
（3）若正数a，b，c满足a+b+c=1，求
| 1 |
| 3a+2 |
| 1 |
| 3b+2 |
| 1 |
| 3c+2 |
本题（1）、（2）、（3）三个选答题，每小题7分，请考生任选2题作答，满分14分，如果多做，则按所做的前两题计分。作答时，先用2B铅笔在答题卡上把所选题目对应的题号涂黑，并将所选题号填入括号中.
（1）（本小题满分7分）选修4-4：坐标系与参数方程
以直角坐标系的原点
为极点，
轴的正半轴为极轴。已知点
的直角坐标为（1，-5），点
的极坐标为
若直线
过点，且倾斜角为
，圆
以为圆心、
为半径。
（I）求直线的参数方程和圆的极坐标方程；
（II）试判定直线和圆的位置关系.
（2）（本小题满分7分）选修4-4：矩阵与变换
把曲线
先进行横坐标缩为原来的一半，纵坐标保持不变的伸缩变换，再做关于轴的反射变换变为曲线，求曲线的方程．
（3）（本小题满分7分）选修4-5：不等式选讲
关于的一元二次方程
对任意
无实根，求实数
的取值范围.
查看习题详情和答案>>
三题中任选两题作答
（1）（2011年江苏高考）已知矩阵
，向量
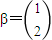，求向量α，使得A2α=β
（2）（2011年山西六校模考）以直角坐标系的原点O为极点，x轴的正半轴为极轴，已知点P的直角坐标为（1，-5），点M的极坐标为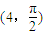
，若直线l过点P，且倾斜角为
，圆C以M为圆心、4为半径．
①求直线l的参数方程和圆C的极坐标方程； ②试判定直线l和圆C的位置关系．
（3）若正数a，b，c满足a+b+c=1，求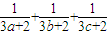
的最小值．
查看习题详情和答案>>
（1）（2011年江苏高考）已知矩阵
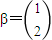，向量，求向量α，使得A2α=β（2）（2011年山西六校模考）以直角坐标系的原点O为极点，x轴的正半轴为极轴，已知点P的直角坐标为（1，-5），点M的极坐标为
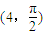，若直线l过点P，且倾斜角为，圆C以M为圆心、4为半径．①求直线l的参数方程和圆C的极坐标方程； ②试判定直线l和圆C的位置关系．
（3）若正数a，b，c满足a+b+c=1，求
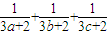的最小值．查看习题详情和答案>>
：
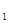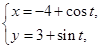（t为参数）， C
：
（
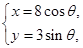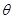为参数）。化C
0, ρ=4sinθ的圆心之间的距离，并判定两圆的位置关系。