题目内容
三题中任选两题作答
(1)(2011年江苏高考)已知矩阵A=
,向量β=
,求向量α,使得A2α=β
(2)(2011年山西六校模考)以直角坐标系的原点O为极点,x轴的正半轴为极轴,已知点P的直角坐标为(1,-5),点M的极坐标为(4,
),若直线l过点P,且倾斜角为
,圆C以M为圆心、4为半径.
①求直线l的参数方程和圆C的极坐标方程; ②试判定直线l和圆C的位置关系.
(3)若正数a,b,c满足a+b+c=1,求
+
+
的最小值.
(1)(2011年江苏高考)已知矩阵A=
|
|
(2)(2011年山西六校模考)以直角坐标系的原点O为极点,x轴的正半轴为极轴,已知点P的直角坐标为(1,-5),点M的极坐标为(4,
| π |
| 2 |
| π |
| 3 |
①求直线l的参数方程和圆C的极坐标方程; ②试判定直线l和圆C的位置关系.
(3)若正数a,b,c满足a+b+c=1,求
| 1 |
| 3a+2 |
| 1 |
| 3b+2 |
| 1 |
| 3c+2 |
分析:(1)设向量
=
,由A2α=β,利用矩阵的运算法则,用待定系数法可得x 和 y 的值,从而求得向量
.
(2)①根据题意直接求直线l的参数方程和圆C的极坐标方程.
②先化直线l的参数方程为普通方程,求出圆心坐标,用圆心的直线距离和半径比较可知位置关系.
(3)利用柯西不等式,即可求得
+
+
的最小值.
| α |
|
| α |
(2)①根据题意直接求直线l的参数方程和圆C的极坐标方程.
②先化直线l的参数方程为普通方程,求出圆心坐标,用圆心的直线距离和半径比较可知位置关系.
(3)利用柯西不等式,即可求得
| 1 |
| 3a+2 |
| 1 |
| 3b+2 |
| 1 |
| 3c+2 |
解答:解:(1)、A2=
•
=
,设向量
=
,由 A2
=
可得
=
,
∴
,解得 x=-1,y=2,
∴向量
=
.
(2)①直线l的参数方程为
,(t为参数)
圆C的极坐标方程为ρ=8sinθ.(6分)
②因为M(4,
)对应的直角坐标为(0,4)
直线l化为普通方程为
x-y-5-
=0
圆心到l的距离d=
=
>4,
所以直线l与圆C相离.(10分)
(3)∵正数a,b,c满足a+b+c=1,
∴(
+
+
)[(3a+2)+(3b+2)+(3c+2)]≥(1+1+1)2,
即
+
+
≥1
当且仅当a=b=c=
时,取等号
∴当a=b=c=
时,
+
+
的最小值为1.
|
|
|
| α |
|
| α |
| β |
|
|
|
∴
|
∴向量
| α |
|
(2)①直线l的参数方程为
|
圆C的极坐标方程为ρ=8sinθ.(6分)
②因为M(4,
| π |
| 2 |
直线l化为普通方程为
| 3 |
| 3 |
圆心到l的距离d=
|0-4-5-
| ||
|
9+
| ||
| 2 |
所以直线l与圆C相离.(10分)
(3)∵正数a,b,c满足a+b+c=1,
∴(
| 1 |
| 3a+2 |
| 1 |
| 3b+2 |
| 1 |
| 3c+2 |
即
| 1 |
| 3a+2 |
| 1 |
| 3b+2 |
| 1 |
| 3c+2 |
当且仅当a=b=c=
| 1 |
| 3 |
∴当a=b=c=
| 1 |
| 3 |
| 1 |
| 3a+2 |
| 1 |
| 3b+2 |
| 1 |
| 3c+2 |
点评:本题考查圆与圆的位置关系,参数方程与普通方程的互化,矩阵的运算法则,绝对值不等式的解法.第(3)小题考查求最小值,解题的关键是利用柯西不等式进行求解,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 三选一题(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
三选一题(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)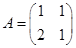 ,向量
,向量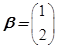 ,求向量
,求向量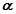 ,使得
,使得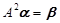
 ,向量
,向量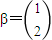 ,求向量α,使得A2α=β
,求向量α,使得A2α=β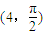 ,若直线l过点P,且倾斜角为
,若直线l过点P,且倾斜角为 ,圆C以M为圆心、4为半径.
,圆C以M为圆心、4为半径.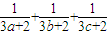 的最小值.
的最小值.