网址:http://m.1010jiajiao.com/timu_id_310512[举报]
(1)求实数t的取值范围;
(2)是否存在实数t,使得线段AB(包括两端点)与直线x=1相交?若存在,求出t的取值范围;若不存在,请说明理由.
(文)已知函数f(x)=mx3-x的图像上,以N(1,n)为切点的切线的倾斜角为![]() .
.
(1)求m,n的值;
(2)是否存在最小的正整数k,使得不等式f(x)≤k-1991对于x∈[-1,3]恒成?如果存在,请求出最小的正整数k;如果不存在,请说明理由。
(3)求证:|f(sinx)+f(cosx)|≤2f(t+![]() )(x∈R,t>0).
)(x∈R,t>0).
(1)求{f(n)}、{g(n)}的通项公式;
(2)设cn=g[![]() f(n)],求数列{cn}的前n项和;
f(n)],求数列{cn}的前n项和;
(3)已知![]() =0,设F(n)=Sn-3n,是否存在整数m和M,使得对任意正整数n,不等式m<F(n)<M恒成立?若存在,分别求出m和M的集合,并求出M-m的最小值;若不存在,请说明理由.
=0,设F(n)=Sn-3n,是否存在整数m和M,使得对任意正整数n,不等式m<F(n)<M恒成立?若存在,分别求出m和M的集合,并求出M-m的最小值;若不存在,请说明理由.
(文)已知f(x)=![]() x3-3x,g(x)=2ax2.
x3-3x,g(x)=2ax2.
(1)当-![]() ≤a≤
≤a≤![]() 时,求证:F(x)=f(x)-g(x)在(-1,1)上是单调函数;
时,求证:F(x)=f(x)-g(x)在(-1,1)上是单调函数;
(2)若g′(x)≤![]() 〔g′(x)为g(x)的导函数〕在[-1,
〔g′(x)为g(x)的导函数〕在[-1,![]() ]上恒成立,求a的取值范围.
]上恒成立,求a的取值范围.
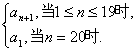 确定.记M=
确定.记M=(1)当k=1时,求M的值;
(2)求M的最小值及相应的k的值.
(文)设数列{an}的首项a1=a(a∈R),且an+1=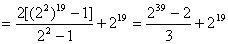 n=1,2,3,….
n=1,2,3,….
(1)若0<a<1,求a2、a3、a4、a5;
(2)若0<an<4,证明0<an+1<4;
(3)若0<a≤2,求所有的正整数k,使得对于任意n∈N*,均有an+k=an成立.
查看习题详情和答案>>(1)设{bn}是项数为7的“对称数列”,其中b1,b2,b3,b4是等差数列,且b1=2,b4=11.依次写出{bn}的每一项.
(2)设{cn}是项数为2k-1(正整数k>1)的“对称数列”,其中ck,ck+1,…,c2k-1是首项为50,公差为-4的等差数列.记{cn}各项的和为S2k-1,当k为何值时,S2k-1取得最大值?并求出S2k-1的最大值.
(3)对于确定的正整数m>1,写出所有项数不超过2m的“对称数列”,使得1,2,22,…,2m-1依次是该数列中连续的项;当m>1 500时,求其中一个“对称数列”前2 008项的和S2008.
(文)如果有穷数列a1,a2,a3,…,am(m为正整数)满足条件a1=am,a2=am-1,…,am=a1,即ai=am-i+1(i=1,2,…,m),我们称其为“对称数列”.例如,数列1,2,5,2,1与数列8,4,2,2,4,8都是“对称数列”.
(1)设{bn}是7项的“对称数列”,其中b1,b2,b3,b4是等差数列,且b1=2,b4=11.依次写出{bn}的每一项;
(2)设{cn}是49项的“对称数列”,其中c25,c26,…,c49是首项为1,公比为2的等比数列,求{cn}各项的和S;
(3)设{dn}是100项的“对称数列”,其中d51,d52,…,d100是首项为2,公差为3的等差数列,求{dn}前n项的和Sn(n=1,2,…,100).
查看习题详情和答案>>