题目内容
(理)设a1,a2,…,a20是首项为1,公比为2的等比数列.对于满足0≤k≤19的整数k,数列b1,b2,…,b20由bn=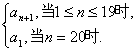 确定.记M=
确定.记M=(1)当k=1时,求M的值;
(2)求M的最小值及相应的k的值.
(文)设数列{an}的首项a1=a(a∈R),且an+1=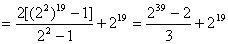 n=1,2,3,….
n=1,2,3,….
(1)若0<a<1,求a2、a3、a4、a5;
(2)若0<an<4,证明0<an+1<4;
(3)若0<a≤2,求所有的正整数k,使得对于任意n∈N*,均有an+k=an成立.
答案:(理)解:(1)显然an=2n-1,其中1≤n≤20.
当k=1时,bn=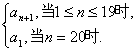 .
.
所以,![]()
![]() .
.
(2)M=![]()
![]()
![]() =
=![]() (40-k-2k)+
(40-k-2k)+![]() (220+k-220-k)
(220+k-220-k)
=![]() .
.
当2k=![]() ,即k=10时,M=
,即k=10时,M=![]() .
.
所以M的最小值为![]() ,此时k=10.
,此时k=10.
(文)(1)解:因为a1=a∈(0,1),所以a2=-a1+4=-a+4,且a2∈(3,4).所以a3=a2-3=-a+1,且a3∈(0,1).所以a4=-a3+4=a+3,且a4∈(3,4).所以a5=a4-3=a.
(2)证明:①当0<an≤3时,an+1=-an+4,所以1≤an+1<4.
②当3<an<4时,an+1=an-3,所以0<an+1<1.综上,0<an<4时,0<an+1<4.
(3)解:①若0<a<1,由(1),知a5=a1,所以k=4;因此,当k=4m(m∈N*)时,对所有的n∈N*,an+k=an成立.
②若1≤a<2,则a2=-a+4,且a2∈(2,3],a3=-a2+4=-(-a+4)+4=a=a1,所以k=2;因此,当k=2m(m∈N*)时,对所有的n∈N*,an+k=an成立.
③若a=2,则a2=a3=a4=…,所以k=1.因此,当k=m(m∈N*)时,对所有的n∈N*,an+k=an成立.
综上,若0<a<1,则k=4m;若1≤a<2,则k=2m;若a=2,则k=m(m∈N*).

练习册系列答案
相关题目
