摘要：设动圆M的圆心由|AB|=2.可知点B在圆A内.从而圆M内切于圆A.故|MA|=r1―r2.即|MA|+|MB|=4.所以.点M的轨迹是以A.B为焦点的椭圆.
网址：http://m.1010jiajiao.com/timu_id_310320[举报]
已知点P在定圆O的圆内或圆周上，动圆C过点P与定圆O相切，则动圆C的圆心轨迹可能是已知点P在定圆O的圆内或圆周上，动圆C过点P与定圆O相切，则动圆C的圆心轨迹可能是
- A.圆或椭圆或双曲线
- B.两条射线或圆或抛物线
- C.两条射线或圆或椭圆
- D.椭圆或双曲线或抛物线
已知：三定点A(-
，0)，B(
，0)，C(-
，0)，动圆M线AB相切于N，且|AN|-|BN|=
，现分别过点A、B作动圆M的切线，两切线交于点P．
（1）求动点P的轨迹方程；
（2）直线3x-3my-2截动点P的轨迹所得弦长为2，求m的值；
（3）是否存在常数λ，使得∠PBC=λ∠PCB，若存在，求λ的值，若不存在，并请说明理由． 查看习题详情和答案>>
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
（1）求动点P的轨迹方程；
（2）直线3x-3my-2截动点P的轨迹所得弦长为2，求m的值；
（3）是否存在常数λ，使得∠PBC=λ∠PCB，若存在，求λ的值，若不存在，并请说明理由． 查看习题详情和答案>>
（2010•石家庄二模）已知动圆M经过点G（0，-1），且与圆Q：x2+（y-1）2=8内切．
（Ⅰ）求动圆M的圆心的轨迹E的方程．
（Ⅱ）以m=(1，
)为方向向量的直线l交曲线E于不同的两点A、B，在曲线E上是否存在点P使四边形OAPB为平行四边形（O为坐标原点）．若存在，求出所有的P点的坐标与直线l的方程；若不存在，请说明理由．
查看习题详情和答案>>
（Ⅰ）求动圆M的圆心的轨迹E的方程．
（Ⅱ）以m=(1，
| 2 |
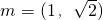为方向向量的直线l交曲线E于不同的两点A、B，在曲线E上是否存在点P使四边形OAPB为平行四边形（O为坐标原点）．若存在，求出所有的P点的坐标与直线l的方程；若不存在，请说明理由．