网址:http://m.1010jiajiao.com/timu_id_300722[举报]
一
1.C 2.B 3.C 4.C 5.A 6.D 7.C 8.B 9.B 10.B
二
11.3.files/image072.gif) 12. 360°-36°?n 13.
12. 360°-36°?n 13.
三
17.∵(x+5)(x+7)=(x2+12x+35+1-1)=(x+6)2-1<(x+6)2
∴(x+5)(x+7)< (x+6)2
18.(1)图略 …………………… 3分
(2)12个单位 ……………… 6分
19.解:连接DE,BF.
∵四边形ABCD是矩形,
∴AB∥CD. ∠ODF=∠OBE ………… 1分
∵EF垂直平分BD,
∴OD=
∴ΔDOF≌ΔBOE(ASA) ……… 2分
∴DF=BE
∴四边形BFDE是平行四边形。
∵EF.files/image016.gif) 垂直平分BD,
垂直平分BD,
FD=FB(线段的垂直平分线上的点到线段两端点的距离相等)
∴平行四边形BFDE是菱形 ……… 4分
∴DF=BF=DE=EB,OE=OF.
在RtΔDOF中,DF=.files/image074.gif)
.files/image076.gif) +
+.files/image078.gif) =250
=250
∴S菱形DEBF=.files/image080.gif) BD?EF=DF?BC
BD?EF=DF?BC
∴.files/image080.gif) Х400х300=250?BC
Х400х300=250?BC
∴BC=240 ………… 5分
在RtΔBCF中 FC=.files/image083.gif) =
=.files/image085.gif) =70
=70
∴CD=DF+FC=250+70=320
∴S梯形ABCD=CD?BC=320×240=
答略 …………… 7分
20.解:将圆柱有相对的A.B垂直切开,并将半圆柱侧面展开成一个矩形, ……… 2分
如图所示,作BO⊥AO于O,则AO,BO分别平行于矩形的两边,作A点关于D点的对称点Aㄆ,连AㄆB,则ΔA`
.files/image087.jpg) BO为直角三角形,且BO=
BO为直角三角形,且BO=.files/image089.gif) =12,A`O=(15-3)+4=16, ………… 4分
=12,A`O=(15-3)+4=16, ………… 4分
有勾股定理得
A`B2=A´O2+BO2=162+122=400,
∴A´B=20 ……………… 7分
故蜘蛛沿B外_壁C内_壁A路线爬行最近,
且它至少要走
21.因为.files/image091.gif) 0.1x+0.01x2,而
0.1x+0.01x2,而.files/image091.gif) 12,所以0.1x+0.01x2=12,……………… 2分
12,所以0.1x+0.01x2=12,……………… 2分
解之,得.files/image093.gif) ,
,.files/image095.gif) 舍去,故
舍去,故.files/image097.gif) <40,
<40,
所以甲车未超速行驶。 ……………………………………………… 4分
设.files/image099.gif) =kx,把(60,15)代入,得 15=60k。解得,k=
=kx,把(60,15)代入,得 15=60k。解得,k=.files/image101.gif) 。
。
故.files/image099.gif) =
=.files/image101.gif) x.
……………………………………………… 6分
x.
……………………………………………… 6分
由题意知 10<.files/image101.gif) x<12解之得:40<x<48.
x<12解之得:40<x<48.
所以乙车超速行驶。……………………………………………… 8分
22.(1)∵a2=b2+c2-2bccosA=25+49-2?5?7?cos60º= 39
∴a=.files/image103.gif) …………… 2分
…………… 2分
∵b2=a2+c2-2accosB.
∴cosB=.files/image105.gif) =
=.files/image107.gif)
∠B≈36º …………… 3分
∴∠C=180º-60º-36º=84º …………… 4分
(2).由余弦定理得 72=82+92-2×8×9cosA
得 cosA=.files/image109.gif)
∴∠A≈48º ………… 6分
再得 82=92+72-2×9×7cosB
得 cosB=.files/image111.gif)
∠B≈58º ……………… 7分
∴∠C=180º-∠A-∠B=74º ……… 8分
23.(1).连接BE,可得ΔABE∽ΔADB. ……………… 2分
∴ AB2=AD?AE ……………… 4分
(2).成立 ……………… 5分
连接EB,可证ΔAEB∽ΔABD, ……………… 7分
∴仍可得AB2=AD?AE …………… 8分
24.(1)y=60-(x-100).files/image113.gif) 0.02x (0<x<550)
………………
4分
0.02x (0<x<550)
………………
4分
(2)根据题意可列方程为:6000=[60-(x-100)0.02]x-40x
整理可得:x2-3100x+300000=0 ………………. 6分
(x-500)(x-600)=0 ………… 8分
x1=500 x2=600(舍去) ……………… 9分
销售商订购500个时,该厂可获利润6000元。 ………. 10分
25.(1)S梯形OPFE=.files/image080.gif) (OP+EF)?OE=
(OP+EF)?OE=.files/image080.gif) (25+27)
(25+27).files/image117.gif)
设运动时间为t秒时,梯形OPFE的面积为y
则y=.files/image080.gif) (28-3t+28-t)t=-2t2+28t=-2(t-7)2+98. ……………… 3分
(28-3t+28-t)t=-2t2+28t=-2(t-7)2+98. ……………… 3分
所以当t=7秒时,梯形OPFE的面积最大,最大面积为98; ……………… 4分
(2)当S梯形OPFE=SΔAPF时,
-2t2+28t=.files/image119.gif) ,解得t1=8,t2=0(舍去)。
…………… 7分
,解得t1=8,t2=0(舍去)。
…………… 7分
当t=8秒时,FP=8.files/image121.gif) ……………… 8分
……………… 8分
(3) 由.files/image123.gif) ,
……………… 10分
,
……………… 10分
且∠OAB=∠OAB, ……… 11分
可证得ΔAF1P1.files/image016.gif) ∽ΔAF2P2
…… 12分
∽ΔAF2P2
…… 12分
 如图,在Rt△ABC中,AC=2AB,∠BAC=90°,D是AC的中点,在Rt△DEA中,∠AED=90°,∠EAD=45°,连结BE、CE,试猜想BE和EC的关系,并证明你的猜想.
如图,在Rt△ABC中,AC=2AB,∠BAC=90°,D是AC的中点,在Rt△DEA中,∠AED=90°,∠EAD=45°,连结BE、CE,试猜想BE和EC的关系,并证明你的猜想.(1)猜想:
(2)证明:
∴∠EAD=∠EDA=45°,
∴AE=DE,
∵∠BAC=90°,
∴∠EAB=∠EAD+∠BAC=45°+90°=135°,
∠EDC=∠ADC-∠EDA=180°-45°=135°,
∴∠EAB=∠EDC,
∵D是AC的中点,
∴AD=CD=
| 1 |
| 2 |
∵AC=2AB,
∴AB=AD=DC,
∵在△EAB和△EDC中,
|
∴△EAB≌△EDC(SAS),
∴EB=EC,且∠AEB=∠DEC,
∴∠BEC=∠DEC+∠BED=∠AEB+∠BED=∠AED=90°,
∴BE⊥EC
∴∠EAD=∠EDA=45°,
∴AE=DE,
∵∠BAC=90°,
∴∠EAB=∠EAD+∠BAC=45°+90°=135°,
∠EDC=∠ADC-∠EDA=180°-45°=135°,
∴∠EAB=∠EDC,
∵D是AC的中点,
∴AD=CD=
| 1 |
| 2 |
∵AC=2AB,
∴AB=AD=DC,
∵在△EAB和△EDC中,
|
∴△EAB≌△EDC(SAS),
∴EB=EC,且∠AEB=∠DEC,
∴∠BEC=∠DEC+∠BED=∠AEB+∠BED=∠AED=90°,
∴BE⊥EC
 如图,在Rt△ABC中,∠C=90°,AB的垂直平分线与BC,AB的交点分别为D,E.
如图,在Rt△ABC中,∠C=90°,AB的垂直平分线与BC,AB的交点分别为D,E.(1)若AD=10,sin∠ADC=
| 4 |
| 5 |
(2)若AD=1,∠ADC=α,参考(1)的计算过程直接写出tan
| α |
| 2 |
(1)如图(1),我们已经学习了直角三角形中的边角关系,在Rt△ACD中,sin∠A=
| 1 |
| 2 |
(2)如图(2),在△ABC中,CD⊥AB于D,∠ACD=α,∠DCB=β.
∵S△ABC=S△ADC+S△BDC,由公式①,得
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
请你利用直角三角形边角关系,消去②中的AC、BC、CD,将得到新的结论.并写出解决过程.
(3)利用(2)中的结论,试求sin75°和sin105°的值,并比较其大.
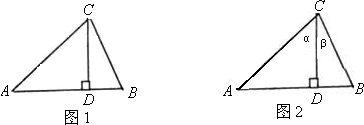 查看习题详情和答案>>
查看习题详情和答案>>
编写要求:①提出具有综合性、连续性的三个问题;②给出正确的解答过程;③写出编写意图和学生答题情况的预测.
材料①:如图,先把一矩形纸片ABCD对折,得到折痕MN,然后把B点叠在折痕线上,得到△ABE,再过点B把矩形ABCD第三次折叠,使点D落在直线AD上,得到折痕PQ.当沿着BE第四次将该纸片折叠后,点A就会落在EC上.
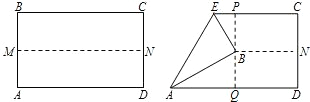
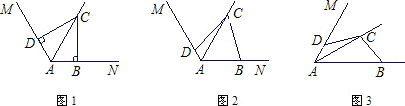
材料②:已知AC是∠MAN的平分线.
(1)在图1中,若∠MAN=120°,∠ABC=ADC=90°,求证:AB+AD=AC;
(2)在图2中,若∠MAN=120°,∠ABC+∠ADC=180°,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由;
(3)在图3中:若∠MAN=α(0°<α<180°),∠ABC+∠ADC=180°,
则AB+AD=
材料③:
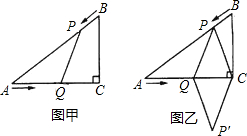
已知:如图甲,在Rt△ACB中,∠C=90°,AC=4cm,BC=3cm,点P由B出发沿线段BA向点A匀速运动,速度为1cm/s;点Q由A出发沿线段AC向点C匀速运动,速度为2cm/s;连接PQ,设运动的时间为t(s)(0<t<2).
编写试题选取的材料是
编写的试题是:(1)设△AQP的面积为y(cm2),求y与t之间的函数关系式.
(2)是否存在某一时刻t,使线段PQ恰好把Rt△ACB的周长和面积同时平分?若存在,求出此时t的值.
(3)如图(2),连接PC,并把△PQC沿QC翻折得到四边形PQP'C.是否存在某一时刻t,使四边形PQP'C为菱形?若存在,求出此时菱形的边长.
试题解答(写出主要步骤即可):(1)过点Q作QD⊥AP于点D,证△AQD∽△ABC,利用相似性质及面积解答;
(2)分别求得Rt△ACB的周长和面积,由周长求出t,代入函数解析式验证;
(3)利用余弦定理得出PC、PQ,联立方程,求得t,再代入PC解得答案. 查看习题详情和答案>>
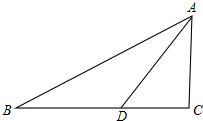 (2012•葫芦岛)如图,在Rt△ABC中,∠C=90°,BC=8,tanB=
(2012•葫芦岛)如图,在Rt△ABC中,∠C=90°,BC=8,tanB=