题目内容
(2012•顺河区一模)设函数f(x)=|2x-m|+4x.
(I)当m=2时,解不等式:f(x)≤1;
(Ⅱ)若不等式f(x)≤2的解集为{x|x≤-2},求m的值.
(I)当m=2时,解不等式:f(x)≤1;
(Ⅱ)若不等式f(x)≤2的解集为{x|x≤-2},求m的值.
分析:(I)当m=2时,函数f(x)=|2x-2|+4x,由不等式f(x)≤1 可得 ①
,或 ②
,分别求出①②的解集,再取并集,即得所求.
(Ⅱ)由f(x)=
,可得连续函数f(x) 在R上是增函数,故有f(-2)=2,分当
≥-2和当
<-2两种情况,分别求出m的值,即为所求.
|
|
(Ⅱ)由f(x)=
|
| m |
| 2 |
| m |
| 2 |
解答:解:(I)当m=2时,函数f(x)=|2x-2|+4x,由不等式f(x)≤1 可得 ①
,或 ②
.
解①可得x∈∅,解②可得x≤-
,故不等式的解集为 {x|x≤-
}.
(Ⅱ)∵f(x)=
,连续函数f(x) 在R上是增函数,由于f(x)≤2的解集为{x|x≤-2},
故f(-2)=2,当
≥-2时,有2×(-2)+m=2,解得 m=6.
当
<-2时,则有6×(-2)-m=2,解得 m=-14.
综上可得,当 m=6或 m=-14 时,f(x)≤2的解集为{x|x≤-2}.
|
|
解①可得x∈∅,解②可得x≤-
| 1 |
| 2 |
| 1 |
| 2 |
(Ⅱ)∵f(x)=
|
故f(-2)=2,当
| m |
| 2 |
当
| m |
| 2 |
综上可得,当 m=6或 m=-14 时,f(x)≤2的解集为{x|x≤-2}.
点评:本题主要考查带有绝对值的函数,绝对值不等式的解法,体现了分类讨论的数学思想,属于中档题.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
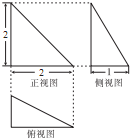 (2012•顺河区一模)三棱椎A-BCD的三视图为如图所示的三个直角三角形,则三棱锥A-BCD的表面积为( )
(2012•顺河区一模)三棱椎A-BCD的三视图为如图所示的三个直角三角形,则三棱锥A-BCD的表面积为( )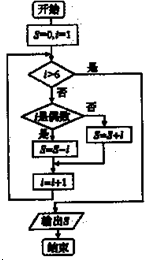 (2012•顺河区一模)执行如图所给的程序框图,则运行后输出的结果是( )
(2012•顺河区一模)执行如图所给的程序框图,则运行后输出的结果是( )