题目内容
已知函数f(x)=|x-a|-|x-5|,a>0.
(I)若a=2,求f(x)≥0的解集.
(II)若不等式f(x)≤2x的解集为[5,+∞),求a的值.
(I)若a=2,求f(x)≥0的解集.
(II)若不等式f(x)≤2x的解集为[5,+∞),求a的值.
分析:(I)当a=2时,ff(x)≥0可化为|x-2|≥|x-5|,直接求出不等式|x-2|≥|x-5|的解集即可.
(II)由题设知:|x-a|-|x-5|≤2x.下面就a的取值分类讨论,在同一坐标系中作出函数y=f(x)和y=2x的图象,结合图象即可求得 a 的值.
(II)由题设知:|x-a|-|x-5|≤2x.下面就a的取值分类讨论,在同一坐标系中作出函数y=f(x)和y=2x的图象,结合图象即可求得 a 的值.
解答:解:( I) a=2时,f(x)=|x-2|-|x-5|,f(x)≥0,
即|x-2|≥|x-5|,x≥
,所以f(x)≥0的解集[
,+∞).
( II) f(x)≤2x即|x-a|-|x-5|≤2x ①
(1)a=5时,解①得x≥0,不合题意.
(2)a>5时,f(x)=
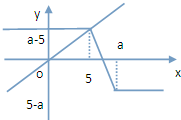
函数图象如图,
∵f(x)≤2x的解集为[5,+∞),
∴直线y=2x过(5,a-5),
∴a-5=10,a=15.
(3)0<a<5时,f(x)=
函数图象如下图,不合题意.
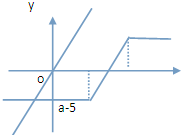
综上,a=15.
即|x-2|≥|x-5|,x≥
| 7 |
| 2 |
| 7 |
| 2 |
( II) f(x)≤2x即|x-a|-|x-5|≤2x ①
(1)a=5时,解①得x≥0,不合题意.
(2)a>5时,f(x)=
|

函数图象如图,
∵f(x)≤2x的解集为[5,+∞),
∴直线y=2x过(5,a-5),
∴a-5=10,a=15.
(3)0<a<5时,f(x)=
|
函数图象如下图,不合题意.

综上,a=15.
点评:本题考查绝对值不等式的解法,函数图象的特征,体现了数形结合的数学思想,画出函数f(x)的图象,是解题的关键.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|