网址：http://m.1010jiajiao.com/timu_id_28578[举报]
一、选择题：本大题共10个小题，每小题5分，共50分．
题号
1
2
3
4
5
6
7
8
9
10
答案
C
B
C
D
C
B
A
D
B
A
二、填空题：本大题共4个小题，每小题4分，共16分．
11. 630 12. 2k 13. 
14. ①②③
三、解答题：本大题共6个小题，每小题14分，共84分．
15．
(4分) 
由题意得
16． 
有分布列：
0
1
2
3
P
从而期望
17．（1）
又
(2) 
(3)DE//AB,
(4)设BB1的中点为F，连接EF、DF，则EF是DF在平面BB
因为BB
18.(1) 由题意得
(2) 
所以直线
的斜率为
令
，则直线的斜率
，
19．（1）由韦达定理得
是首项为4，公差为2的等差数列。
（2）由（1）知
，则
原式左边=
=
=右式。故原式成立。
20．令x=y=0，有
，令y=-x则
得
故（1）得证。
（2）在R上任取x1,x2且
，且
，
所以
在R上单调递增；
（3）
由
得
；
由
得
；因为
，
所以
无解，即圆心到直线的距离大于或等于半径2，只需
| S(k+1)n |
| Skn |
（1）已知Sn=
| 4 |
| 3 |
| 2 |
| 3 |
（2）在（1）的条件下，数列an=2cn，求证数列cn是一个“1 类和科比数列”（4分）；
（3）设等差数列{bn}是一个“k类和科比数列”，其中首项b1，公差D，探究b1与D的数量关系，并写出相应的常数t=f（k）． 查看习题详情和答案>>
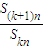是与n无关的非零常数t=f（k），则称该数列{an}是“k类和科比数列”．（1）已知
，求数列{an}的通项公式；（2）在（1）的条件下，数列
，求证数列cn是一个“1 类和科比数列”（4分）；（3）设等差数列{bn}是一个“k类和科比数列”，其中首项b1，公差D，探究b1与D的数量关系，并写出相应的常数t=f（k）．
查看习题详情和答案>>
数列{an}的前n项和记为Sn，前kn项和记为
Skn(n，k∈N*)，对给定的常数k，若
是与n无关的非零常数t＝f(k)，则称该数列{an}是“k类和科比数列”，
(1)已知Sn＝
an－
(n∈N*)，求数列{an}的通项公式；
(2)在(1)的条件下，数列an＝2cn，求证数列{cn}是一个“1类和科比数列”；
(3)、设等差数列{bn}是一个“k类和科比数列”，其中首项b1，公差D，探究b1
与D的数量关系，并写出相应的常数t＝f(k)；
．
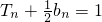