摘要:∴的轨迹方程为. ----3分
网址:http://m.1010jiajiao.com/timu_id_284117[举报]
已知动点P的轨迹方程为:
-
=1(x>2),O是坐标原点.
①若直线x-my-3=0截动点P的轨迹所得弦长为5,求实数m的值;
②设过P的轨迹上的点P的直线与该双曲线的两渐近线分别交于点P1、P2,且点P分有向线段
所成的比为λ(λ>0),当λ∈[
,
]时,求|
|•|
|的最值.
查看习题详情和答案>>
| x2 |
| 4 |
| y2 |
| 5 |
①若直线x-my-3=0截动点P的轨迹所得弦长为5,求实数m的值;
②设过P的轨迹上的点P的直线与该双曲线的两渐近线分别交于点P1、P2,且点P分有向线段
| P1P2 |
| 3 |
| 4 |
| 3 |
| 2 |
| OP1 |
| OP2 |
已知动点P的轨迹方程为: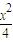 -
-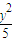 =1(x>2),O是坐标原点.
=1(x>2),O是坐标原点.
①若直线x-my-3=0截动点P的轨迹所得弦长为5,求实数m的值;
②设过P的轨迹上的点P的直线与该双曲线的两渐近线分别交于点P1、P2,且点P分有向线段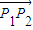 所成的比为λ(λ>0),当λ∈[
所成的比为λ(λ>0),当λ∈[ ,
, ]时,求|
]时,求|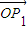 |•|
|•|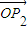 |的最值.
|的最值.
查看习题详情和答案>>
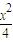 -
-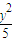 =1(x>2),O是坐标原点.
=1(x>2),O是坐标原点.①若直线x-my-3=0截动点P的轨迹所得弦长为5,求实数m的值;
②设过P的轨迹上的点P的直线与该双曲线的两渐近线分别交于点P1、P2,且点P分有向线段
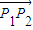 所成的比为λ(λ>0),当λ∈[
所成的比为λ(λ>0),当λ∈[ ,
, ]时,求|
]时,求|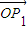 |•|
|•|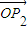 |的最值.
|的最值.查看习题详情和答案>>
已知圆M的方程为:(x+3)2+y2=100及定点N(3,0),动点P在圆M上运动,线段PN的垂直平分线交圆M的半径MP于Q点,设点Q的轨迹为曲线C,则曲线C的方程是
+
=1
+
=1.
查看习题详情和答案>>
| x2 |
| 25 |
| y2 |
| 16 |
| x2 |
| 25 |
| y2 |
| 16 |
 •
•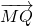 =0成立?若存在,求出实数m的值;若不存在,请说明理由;
=0成立?若存在,求出实数m的值;若不存在,请说明理由; 的垂线PA、QB,垂足分别为A、B,记λ=
的垂线PA、QB,垂足分别为A、B,记λ=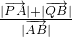 ,求λ,的取值范围.
,求λ,的取值范围.