网址:http://m.1010jiajiao.com/timu_id_280462[举报]
[番茄花园1] (本题满分)在△ABC中,角A,B,C所对的边分别为a,b,c,设S为△ABC的面积,满足 。
。
(Ⅰ)求角C的大小;
(Ⅱ)求 的最大值。
的最大值。
(Ⅰ)解:由题意可知
 absinC=
absinC= ,2abcosC.
,2abcosC.
所以tanC= .
.
因为0<C< ,
,
所以C= .
.
(Ⅱ)解:由已知sinA+sinB=sinA+sin( -C-A)=sinA+sin(
-C-A)=sinA+sin( -A)
-A)
=sinA+ cosA+
cosA+ sinA=
sinA= sin(A+
sin(A+ )≤
)≤ .
.
当△ABC为正三角形时取等号,
所以sinA+sinB的最大值是 .
.
[番茄花园1]1.
查看习题详情和答案>>汕头二中拟建一座长 米,宽
米,宽 米的长方形体育馆.按照建筑要求,每隔
米的长方形体育馆.按照建筑要求,每隔 米(
米( ,
, 为正常数)需打建一个桩位,每个桩位需花费
为正常数)需打建一个桩位,每个桩位需花费 万元(桩位视为一点且打在长方形的边上),桩位之间的
万元(桩位视为一点且打在长方形的边上),桩位之间的 米墙面需花
米墙面需花 万元,在不计地板和天花板的情况下,当
万元,在不计地板和天花板的情况下,当 为何值时,所需总费用最少?
为何值时,所需总费用最少?
【解析】本试题主要考查了导数在研究函数中的运用。先求需打 个桩位.再求解墙面所需费用为:
个桩位.再求解墙面所需费用为: ,最后表示总费用
,最后表示总费用 ,利用导数判定单调性,求解最值。
,利用导数判定单调性,求解最值。
解:由题意可知,需打 个桩位.
…………………2分
个桩位.
…………………2分
墙面所需费用为: ,……4分
,……4分
∴所需总费用
 (
( )…7分
)…7分
令 ,则
,则
当 时,
时, ;当
;当 时,
时, .
.
∴当 时,
时,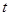 取极小值为
取极小值为 .而在
.而在 内极值点唯一,所以
内极值点唯一,所以 .∴当
.∴当 时,
时, (万元),即每隔3米打建一个桩位时,所需总费用最小为1170万元.
(万元),即每隔3米打建一个桩位时,所需总费用最小为1170万元.
查看习题详情和答案>>
已知函数 (
( 为实数).
为实数).
(Ⅰ)当 时,求
时,求 的最小值;
的最小值;
(Ⅱ)若 在
在 上是单调函数,求
上是单调函数,求 的取值范围.
的取值范围.
【解析】第一问中由题意可知: . ∵
. ∵ ∴
∴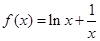 ∴
∴
 .
.
当 时,
时, ;
当
;
当 时,
时, . 故
. 故 .
.
第二问
 .
.
当 时,
时, ,在
,在 上有
上有 ,
, 递增,符合题意;
递增,符合题意;
令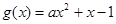 ,则
,则
 ,∴
,∴ 或
或 在
在 上恒成立.转化后解决最值即可。
上恒成立.转化后解决最值即可。
解:(Ⅰ) 由题意可知: . ∵
. ∵ ∴
∴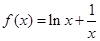 ∴
∴
 .
.
当 时,
时, ;
当
;
当 时,
时, . 故
. 故 .
.
(Ⅱ) 
 .
.
当 时,
时, ,在
,在 上有
上有 ,
, 递增,符合题意;
递增,符合题意;
令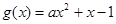 ,则
,则
 ,∴
,∴ 或
或 在
在 上恒成立.∵二次函数
上恒成立.∵二次函数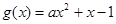 的对称轴为
的对称轴为 ,且
,且
∴ 或
或
 或
或
 或
或
 或
或 . 综上
. 综上
查看习题详情和答案>>
某化工厂生产化工产品,去年生产成本为50元/桶,现使生产成本平均每年降低28%,那么几年后每桶的生产成本为20元(lg2≈0.301 0,lg3≈0.477 1,精确到1年)?
[分析] 设x年后每桶的生产成本为20元,由题意列出关于x,50,28%,20之间的关系式,解出x.
查看习题详情和答案>>已知递增等差数列 满足:
满足: ,且
,且 成等比数列.
成等比数列.
(1)求数列 的通项公式
的通项公式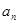 ;
;
(2)若不等式 对任意
对任意 恒成立,试猜想出实数
恒成立,试猜想出实数 的最小值,并证明.
的最小值,并证明.
【解析】本试题主要考查了数列的通项公式的运用以及数列求和的运用。第一问中,利用设数列 公差为
公差为 ,
,
由题意可知 ,即
,即 ,解得d,得到通项公式,第二问中,不等式等价于
,解得d,得到通项公式,第二问中,不等式等价于 ,利用当
,利用当 时,
时, ;当
;当 时,
时, ;而
;而 ,所以猜想,
,所以猜想, 的最小值为
的最小值为 然后加以证明即可。
然后加以证明即可。
解:(1)设数列 公差为
公差为 ,由题意可知
,由题意可知 ,即
,即 ,
,
解得 或
或 (舍去). …………3分
(舍去). …………3分
所以, . …………6分
. …………6分
(2)不等式等价于 ,
,
当 时,
时, ;当
;当 时,
时, ;
;
而 ,所以猜想,
,所以猜想, 的最小值为
的最小值为 . …………8分
. …………8分
下证不等式 对任意
对任意 恒成立.
恒成立.
方法一:数学归纳法.
当 时,
时, ,成立.
,成立.
假设当 时,不等式
时,不等式 成立,
成立,
当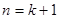 时,
时, ,
…………10分
,
…………10分
只要证  ,只要证
,只要证  ,
,
只要证  ,只要证
,只要证  ,
,
只要证  ,显然成立.所以,对任意
,显然成立.所以,对任意 ,不等式
,不等式 恒成立.…14分
恒成立.…14分
方法二:单调性证明.
要证 
只要证  ,
,
设数列 的通项公式
的通项公式 , …………10分
, …………10分
 , …………12分
, …………12分
所以对 ,都有
,都有 ,可知数列
,可知数列 为单调递减数列.
为单调递减数列.
而 ,所以
,所以 恒成立,
恒成立,
故 的最小值为
的最小值为 .
.
查看习题详情和答案>>