摘要:由三垂线定理.得.
网址:http://m.1010jiajiao.com/timu_id_280239[举报]
 如图,在正三棱柱ABC-A1B1C1中,所有棱的长度都是1,M是BC边的中点,P是AA1边上的点,且PA=
如图,在正三棱柱ABC-A1B1C1中,所有棱的长度都是1,M是BC边的中点,P是AA1边上的点,且PA=
| ||
| 4 |
(1)求:点P到棱BC的距离;
(2)问:在侧棱CC1上是否存在点N,使得异面直线AB1与MN所成角为45°?若存在,请说明点N的位置;若不存在,请说明理由;
(3)定义:如果平面α经过线段AA′的中点,并与线段AA′垂直,则称点A关于平面α的对称点为点A′.设点A关于平面PBC的对称点为A′,求:点A′到平面AMC1的距离.
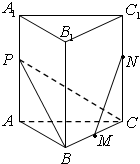
如图,已知三棱柱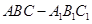 的侧棱与底面垂直,
的侧棱与底面垂直,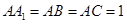 ,
,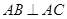 ,
,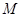 ,
,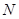 分别是
分别是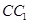 ,
,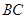 的中点,点
的中点,点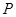 在直线
在直线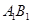 上,且
上,且 ;
;
(Ⅰ)证明:无论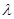 取何值,总有
取何值,总有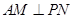 ;
;
(Ⅱ)当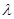 取何值时,直线
取何值时,直线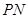 与平面
与平面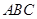 所成的角
所成的角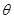 最大?并求该角取最大值时的正切值;
最大?并求该角取最大值时的正切值;
(Ⅲ)是否存在点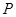 ,使得平面
,使得平面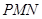 与平面
与平面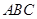 所成的二面角为30º,若存在,试确定点
所成的二面角为30º,若存在,试确定点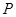 的位置,若不存在,请说明理由.
的位置,若不存在,请说明理由.

查看习题详情和答案>>
如图,已知三棱柱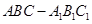 的侧棱与底面垂直,
的侧棱与底面垂直, ,
,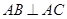 ,
, ,
, 分别是
分别是 ,
, 的中点,点
的中点,点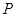 在直线
在直线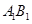 上,且
上,且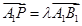 ;
;
(Ⅰ)证明:无论 取何值,总有
取何值,总有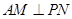 ;
;
(Ⅱ)当 取何值时,直线
取何值时,直线 与平面
与平面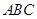 所成的角
所成的角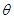 最大?并求该角取最大值时的正切值;
最大?并求该角取最大值时的正切值;
(Ⅲ)是否存在点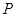 ,使得平面
,使得平面 与平面
与平面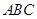 所成的二面角为30º,若存在,试确定点
所成的二面角为30º,若存在,试确定点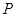 的位置,若不存在,请说明理由.
的位置,若不存在,请说明理由.
 的侧棱与底面垂直,
的侧棱与底面垂直,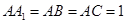 ,
,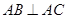 ,
,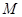 ,
,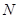 分别是
分别是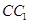 ,
,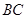 的中点,点
的中点,点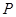 在直线
在直线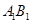 上,且
上,且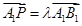 ;
;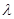 取何值,总有
取何值,总有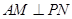 ;
;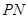 与平面
与平面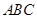 所成的角
所成的角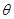 最大?并求该角取最大值时的正切值;
最大?并求该角取最大值时的正切值;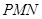 与平面
与平面
