题目内容
如图,已知三棱柱 的侧棱与底面垂直,
的侧棱与底面垂直,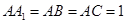 ,
,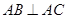 ,
, ,
,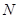 分别是
分别是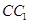 ,
,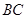 的中点,点
的中点,点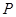 在直线
在直线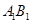 上,且
上,且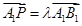 ;
;
(Ⅰ)证明:无论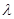 取何值,总有
取何值,总有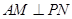 ;
;
(Ⅱ)当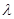 取何值时,直线
取何值时,直线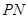 与平面
与平面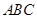 所成的角
所成的角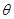 最大?并求该角取最大值时的正切值;
最大?并求该角取最大值时的正切值;
(Ⅲ)是否存在点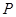 ,使得平面
,使得平面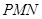 与平面
与平面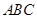 所成的二面角为30º,若存在,试确定点
所成的二面角为30º,若存在,试确定点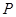 的位置,若不存在,请说明理由.
的位置,若不存在,请说明理由.
 的侧棱与底面垂直,
的侧棱与底面垂直,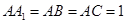 ,
,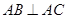 ,
,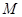 ,
,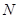 分别是
分别是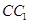 ,
,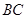 的中点,点
的中点,点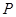 在直线
在直线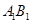 上,且
上,且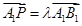 ;
;(Ⅰ)证明:无论
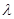 取何值,总有
取何值,总有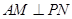 ;
;(Ⅱ)当
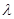 取何值时,直线
取何值时,直线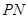 与平面
与平面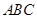 所成的角
所成的角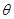 最大?并求该角取最大值时的正切值;
最大?并求该角取最大值时的正切值;(Ⅲ)是否存在点
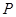 ,使得平面
,使得平面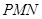 与平面
与平面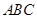 所成的二面角为30º,若存在,试确定点
所成的二面角为30º,若存在,试确定点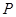 的位置,若不存在,请说明理由.
的位置,若不存在,请说明理由.
(1)略
(2)∴当
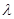 =
=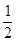 时,θ取得最大值,此时sinθ=
时,θ取得最大值,此时sinθ=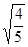 ,cosθ=
,cosθ=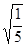 ,tanθ="2"
,tanθ="2" (3)∴不存在点P使得平面PMN与平面ABC所成的二面角为30º
本题主要考查了直线与平面所成的角,以及直线与平面垂直的性质,考查空间想象能力,属于基础题.
(1)以AB,AC,AA1分别为x,y,z轴,建立空间直角坐标系A-xyz,分别求出 PN,AM
的坐标,要证PN⊥AM,只需求证它们的数量积为零即可;
(2)过P作PE⊥AB于E,连接EN,则∠PNE为直线PN与平面ABC所成的角θ,求出此角的正切值,然后研究其最大值即可求出λ的值.
(3)假设存在,则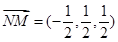 ,设
,设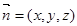 是平面PMN的一个法向量,那么利用向量的坐标得到参数
是平面PMN的一个法向量,那么利用向量的坐标得到参数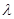 的值,进而判定方程有无解,说明结论。
的值,进而判定方程有无解,说明结论。
(1)以AB,AC,AA1分别为x,y,z轴,建立空间直角坐标系A-xyz,分别求出 PN,AM
的坐标,要证PN⊥AM,只需求证它们的数量积为零即可;
(2)过P作PE⊥AB于E,连接EN,则∠PNE为直线PN与平面ABC所成的角θ,求出此角的正切值,然后研究其最大值即可求出λ的值.
(3)假设存在,则
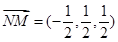 ,设
,设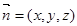 是平面PMN的一个法向量,那么利用向量的坐标得到参数
是平面PMN的一个法向量,那么利用向量的坐标得到参数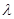 的值,进而判定方程有无解,说明结论。
的值,进而判定方程有无解,说明结论。
练习册系列答案
相关题目
 中,平面
中,平面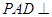 平面
平面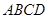 ,
,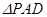 为等边三角形,底面
为等边三角形,底面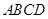 为菱形,
为菱形,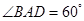 ,
, 为
为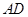 的中点,
的中点,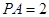 。
。
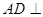 平面
平面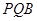 ;
;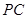 上是否存在点
上是否存在点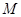 ,使
,使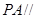 平面
平面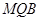 ; 若存在,求出
; 若存在,求出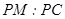 的值。
的值。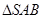 与直角梯形
与直角梯形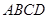 垂直,
垂直,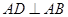 ,
,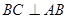 ,
,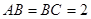 ,
,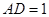 .若
.若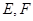 分别为
分别为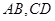 的中点.
的中点.
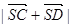 的值; (2)求面
的值; (2)求面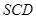 与面
与面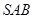 所成的二面角大小.
所成的二面角大小.
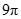
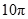
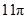
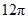
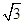
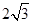
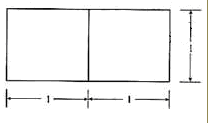


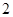 的正三角形,其俯视图轮廓为正方形,则其体积是_________.
的正三角形,其俯视图轮廓为正方形,则其体积是_________.