题目内容
已知A1(x1,y1),A2(x2,y2),…,An(xn,yn)是直线l:y=kx+b上的n个不同的点(n∈N*,k、b均为非零常数),其中数列{xn}为等差数列.(1)求证:数列{yn}是等差数列;
(2)若点P是直线l上一点,且
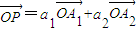 ,求证:a1+a2=1;
,求证:a1+a2=1;(3)设a1+a2+…+an=1,且当i+j=n+1时,恒有ai=aj(i和j都是不大于n的正整数,且i≠j).试探索:在直线l上是否存在这样的点P,使得
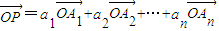 成立?请说明你的理由.
成立?请说明你的理由.
【答案】分析:(1)将yn+1和yn分别代入y=kx+b,令两者相减得定值,便可证明数列{yn}为等差数列;
(2)由题中条件可知PA1A2共线,令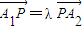 ,即可证明a1+a2=1;
,即可证明a1+a2=1;
(3)先写出满足条件的x的函数,再根据a1+a2+…+an=1和ai=aj及数列{xn}为等差数列等条件逐步化简,便可求出满足条件的P店坐标.
解答:解:(1)证:设等差数列{xn}的公差为d,
∵yn+1-yn=(kxn+1+b)-(kxn+b)=k(xn+1-xn)=kd,
∴yn+1-yn为定值,即数列{yn}是等差数列;
(2)证:因为P、A1和A2都是直线l上一点,故有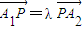 (λ≠-1),
(λ≠-1),
于是,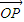 =
= =
=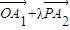 =
= +λ(
+λ(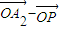 ),
),
∴(1+λ)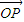 =
=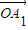 +λ
+λ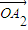
∴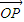 =
=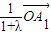 +
+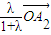 ,
,
令a1= ,a2=
,a2=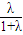 ,则有a1+a2=1;
,则有a1+a2=1;
(3)假设存在点P(x,y),满足要求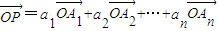 ,
,
则有x=a1x1+a2x2+a3x3+…+anxn,
又当i+j=n+1时,恒有ai=aj,
则又有x=anx1+an-1x2+…+a2xn-1+a1xn,
∴2x=a1(x1+xn)+a2(x2+xn-1)+a3(x3+xn-2)+…+an(xn+x1),
又∵数列{xn}为等差数列;
于是x1+xn=x2+xn-1=x3+xn-2=…=xn+x1
∴2x=(a1+a2+a3+…+an)(x1+xn)=x1+xn
故x= ,同理y=
,同理y=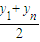 ,
,
且点P(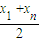 ,
, )在直线上(是A1、An的中点),
)在直线上(是A1、An的中点),
即存在点P( ,
,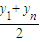 )满足要求.
)满足要求.
点评:本题主要考查了等差数列与向量的综合运用,是各地高考的热点,综合性较强,考查了学生对知识的综合运用和全面掌握,平常应多加训练.
(2)由题中条件可知PA1A2共线,令
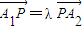 ,即可证明a1+a2=1;
,即可证明a1+a2=1;(3)先写出满足条件的x的函数,再根据a1+a2+…+an=1和ai=aj及数列{xn}为等差数列等条件逐步化简,便可求出满足条件的P店坐标.
解答:解:(1)证:设等差数列{xn}的公差为d,
∵yn+1-yn=(kxn+1+b)-(kxn+b)=k(xn+1-xn)=kd,
∴yn+1-yn为定值,即数列{yn}是等差数列;
(2)证:因为P、A1和A2都是直线l上一点,故有
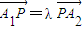 (λ≠-1),
(λ≠-1),于是,
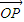 =
= =
=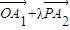 =
= +λ(
+λ(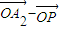 ),
),∴(1+λ)
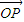 =
=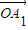 +λ
+λ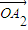
∴
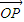 =
=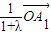 +
+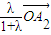 ,
,令a1=
 ,a2=
,a2=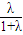 ,则有a1+a2=1;
,则有a1+a2=1;(3)假设存在点P(x,y),满足要求
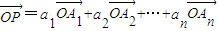 ,
,则有x=a1x1+a2x2+a3x3+…+anxn,
又当i+j=n+1时,恒有ai=aj,
则又有x=anx1+an-1x2+…+a2xn-1+a1xn,
∴2x=a1(x1+xn)+a2(x2+xn-1)+a3(x3+xn-2)+…+an(xn+x1),
又∵数列{xn}为等差数列;
于是x1+xn=x2+xn-1=x3+xn-2=…=xn+x1
∴2x=(a1+a2+a3+…+an)(x1+xn)=x1+xn
故x=
 ,同理y=
,同理y=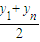 ,
,且点P(
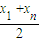 ,
, )在直线上(是A1、An的中点),
)在直线上(是A1、An的中点),即存在点P(
 ,
,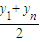 )满足要求.
)满足要求.点评:本题主要考查了等差数列与向量的综合运用,是各地高考的热点,综合性较强,考查了学生对知识的综合运用和全面掌握,平常应多加训练.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
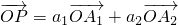 ,求a1+a2的值;
,求a1+a2的值;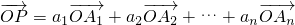 ,我们称
,我们称 是向量
是向量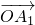 ,
, ,…,
,…,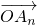 的线性组合,{an}是该线性组合的系数数列.当
的线性组合,{an}是该线性组合的系数数列.当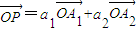 ,求a1+a2的值;
,求a1+a2的值;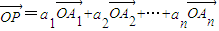 ,我们称
,我们称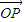 是向量
是向量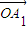 ,
,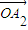 ,…,
,…,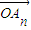 的线性组合,{an}是该线性组合的系数数列.当
的线性组合,{an}是该线性组合的系数数列.当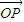 是向量
是向量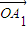 ,
,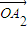 ,…,
,…,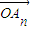 的线性组合时,请参考以下线索:
的线性组合时,请参考以下线索: