摘要：8．如图正方体的棱长为.长为的线段的端点在棱上运动.点在正方形内运动.则的中点的轨迹的面积是
网址：http://m.1010jiajiao.com/timu_id_259457[举报]
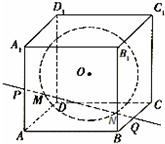如图，在棱长为2的正方体ABCD-A1B1C1D1内有一个内切球O，则过棱AA1和BC的中点P、Q的直线被球面截在球内的线段MN的长为（ ）A、2(
| ||||
B、
| ||||
C、
| ||||
D、
|
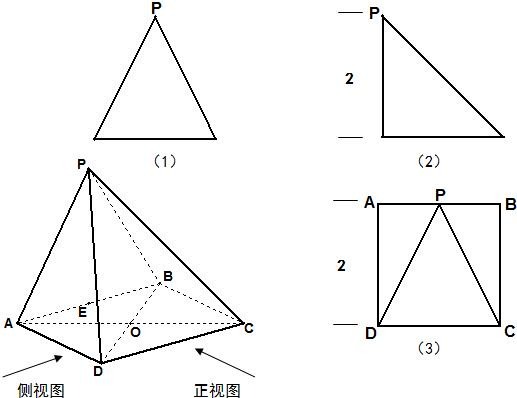
如图四棱锥P-ABCD，它的正视图如图（1），是等腰三角形，
侧视图如图（2），是等腰直角三角形，俯视图如图（3），是正方形ABCD．
各长度如图所示．
（I）求证：平面ADP⊥平面ABP；
（II）设E为AB中点，试在线段PE上确定一点M，使得OM∥平面PDC，并证明；
（III）求四棱锥P-ABCD的体积．
查看习题详情和答案>>
侧视图如图（2），是等腰直角三角形，俯视图如图（3），是正方形ABCD．
各长度如图所示．
（I）求证：平面ADP⊥平面ABP；
（II）设E为AB中点，试在线段PE上确定一点M，使得OM∥平面PDC，并证明；
（III）求四棱锥P-ABCD的体积．
查看习题详情和答案>>
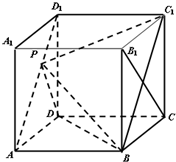如图，在棱长为1的正方体ABCD-A1B1C1D1中，P为线段AD1上的点，且满足| D1P |
| PA |
（Ⅰ）当λ=1时，求证：平面ABC1D1⊥平面PDB；
（Ⅱ）试证无论λ为何值，三棱锥D-PBC1的体积恒为定值；
（Ⅲ）求异面直线C1P与CB1所成的角的余弦值． 查看习题详情和答案>>
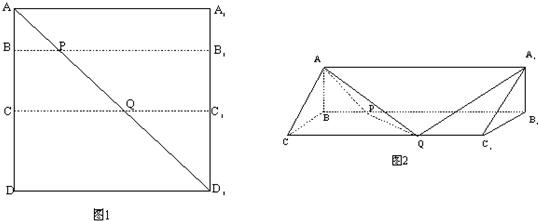
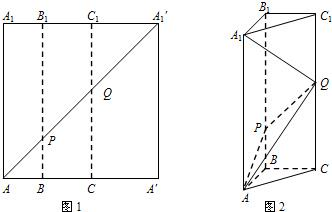如图1所示，在边长为12的正方形AA′A1′A1中，点B，C在线段AA′上，且AB=3，BC=4，作BB1∥AA1，分别交A1A1′、AA1′于点B1、P，作CC1∥AA1，分别交A1A1′、AA1′于点C1、Q，将该正方形沿BB1、CC1折叠，使得A′A1′与AA1重合，构成如图2所示的三棱柱ABC-A1B1C1．