题目内容
 如图,在棱长为1的正方体ABCD-A1B1C1D1中,P为线段AD1上的点,且满足
如图,在棱长为1的正方体ABCD-A1B1C1D1中,P为线段AD1上的点,且满足| D1P |
| PA |
(Ⅰ)当λ=1时,求证:平面ABC1D1⊥平面PDB;
(Ⅱ)试证无论λ为何值,三棱锥D-PBC1的体积恒为定值;
(Ⅲ)求异面直线C1P与CB1所成的角的余弦值.
分析:(I)如图,以点D为坐标原点,建立如图所示的坐标系.当λ=1时,分别求出平面PDB的法向量及平面ABC1D1的法向量,然后代入向量数量积公式,可得两个平面的法向量的数量积为0,由此可得平面ABC1D1⊥平面PDB;
(Ⅱ)根据正方体的几何特征,我们易得三角形PBC1的面积为定值,D到平面PBC1的距离为定值,则三棱锥D-BPC1的体积为定值.
(III)分别确定异面直线C1P与CB1的方向向量(含参数λ),代入数量积公式后,易得两个方向向量的数量积为0,即异面直线C1P与CB1所成的角的余弦值恒为0.
(Ⅱ)根据正方体的几何特征,我们易得三角形PBC1的面积为定值,D到平面PBC1的距离为定值,则三棱锥D-BPC1的体积为定值.
(III)分别确定异面直线C1P与CB1的方向向量(含参数λ),代入数量积公式后,易得两个方向向量的数量积为0,即异面直线C1P与CB1所成的角的余弦值恒为0.
解答:证明:如图,以点D为坐标原点,建立如图所示的坐标系.
(Ⅰ)当λ=1时,即点P为线段AD1的中点,则P(
,0,
),又D(0,0,0)、B(1,1,0)
∴
=(-
,0,-
),
=(
,1,-
),设平面PDB的法向量为
=(x,y,z),…(1分)
则
,即
,令y=1,解得
=(-1,1,1),…(2分)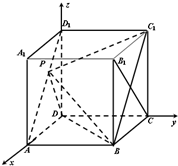
又∵点P为线段AD1的中点,∴DP⊥AD1,∴DP⊥平面ABC1D1,
∴平面ABC1D1的法向量为
=(-
,0,-
),…(3分)
∵
•
=
+0-
=0,
∴平面ABC1D1⊥平面PDB,…(4分)
(Ⅱ)∵AD1∥BC1,P为线段AD1上的点,
∴三角形PBC1的面积为定值,即S△PBC1=
×
×1=
,…(6分)
又∵CD∥平面ABC1D1,
∴点D到平面PBC1的距离为定值,即h=
,…(8分)
∴三棱锥D-BPC1的体积为定值,即VD-PBC1=
•S△PBC1•h=
×
×
=
.
也即无论λ为何值,三棱锥D-PBC1的体积恒为定值
;…(10分)
解:(Ⅲ)∵
=λ
(λ>0),∴P(
,0,
),…(11分)
又C1(0,1,1)、C(0,1,0)、B1(1,1,1),
∴
=(
,-1,
),
=(1,0,1),…(12分)
∵
•
=
+0+
=0…(13分)
∴不管λ取值多少,都有C1P⊥CB1,即异面直线C1P与CB1所成的角的余弦值为0.…(14分)
(Ⅰ)当λ=1时,即点P为线段AD1的中点,则P(
| 1 |
| 2 |
| 1 |
| 2 |
∴
| PD |
| 1 |
| 2 |
| 1 |
| 2 |
| PB |
| 1 |
| 2 |
| 1 |
| 2 |
| n |
则
|
|
| n |

又∵点P为线段AD1的中点,∴DP⊥AD1,∴DP⊥平面ABC1D1,
∴平面ABC1D1的法向量为
| PD |
| 1 |
| 2 |
| 1 |
| 2 |
∵
| PD |
| n |
| 1 |
| 2 |
| 1 |
| 2 |
∴平面ABC1D1⊥平面PDB,…(4分)
(Ⅱ)∵AD1∥BC1,P为线段AD1上的点,
∴三角形PBC1的面积为定值,即S△PBC1=
| 1 |
| 2 |
| 2 |
| ||
| 2 |
又∵CD∥平面ABC1D1,
∴点D到平面PBC1的距离为定值,即h=
| ||
| 2 |
∴三棱锥D-BPC1的体积为定值,即VD-PBC1=
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 6 |
也即无论λ为何值,三棱锥D-PBC1的体积恒为定值
| 1 |
| 6 |
解:(Ⅲ)∵
| D1P |
| PA |
| λ |
| 1+λ |
| 1 |
| 1+λ |
又C1(0,1,1)、C(0,1,0)、B1(1,1,1),
∴
| C1P |
| λ |
| 1+λ |
| -λ |
| 1+λ |
| CB1 |
∵
| C1P |
| CB1 |
| λ |
| 1+λ |
| -λ |
| 1+λ |
∴不管λ取值多少,都有C1P⊥CB1,即异面直线C1P与CB1所成的角的余弦值为0.…(14分)
点评:本题考查的知识点是异面直线及其所成的角,棱锥的体积,平面与平面垂直的判定,(1)(3)的关键是建立空间坐标系,将面面夹角及线线夹角转化为向量夹角问题,(2)的关键是根据正方体的几何特征得到线线平行及线面平行,进而得到点到线,点到面的距离为定值.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
 如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.
如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.
 如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.
如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.
