题目内容
如图1所示,在边长为12的正方形ADD1A1中,点B,C在线段AD上,且AB=3,BC=4,作BB1∥AA1,分别交A1D1,AD1于点B1,P,作CC1∥AA1,分别交A1D1,AD1于点C1,Q,将该正方形沿BB1,CC1折叠,使得DD1与AA1重合,构成如图2所示的三棱柱ABC-A1B1C1.(Ⅰ)求证:AB⊥平面BCC1B1;
(Ⅱ)求四棱锥A-BCQP的体积;
(Ⅲ)求平面PQA与平面BCA所成锐二面角的余弦值.
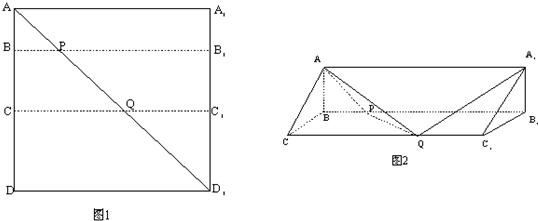
分析:(Ⅰ)证明直线与平面垂直,关键要找到两条相交直线与之都垂直.在这个“折叠问题”中,要把握好不变的长度关系、线线关系、线面关系,比如:AB=3,BC=4,AC=5,所以AB⊥BC;四边形ADD1A1为正方形,AA1∥BB1,所以AB⊥BB1.
(Ⅱ)本题的两问是递进式的,第(1)问是为第(2)问作铺垫的.因为AB⊥平面BCC1B1,所以AB为四棱锥A-BCQP的高,并且四边形BCQP为直角梯形.
(Ⅲ)由(Ⅰ)、(Ⅱ)可知,AB,BC,BB1两两互相垂直.以B为原点,分别以BC、BB1、BA为x、y、z轴,建立如图所示的空间直角坐标系B-xyz,这种解法的好处就是:(1)解题过程中较少用到空间几何中判定线线、面面、线面相对位置的有关定理,因为这些可以用向量方法来解决.(2)即使立体感稍差一些的学生也可以顺利解出,因为只需画个草图以建立坐标系和观察有关点的位置即可.
(Ⅱ)本题的两问是递进式的,第(1)问是为第(2)问作铺垫的.因为AB⊥平面BCC1B1,所以AB为四棱锥A-BCQP的高,并且四边形BCQP为直角梯形.
(Ⅲ)由(Ⅰ)、(Ⅱ)可知,AB,BC,BB1两两互相垂直.以B为原点,分别以BC、BB1、BA为x、y、z轴,建立如图所示的空间直角坐标系B-xyz,这种解法的好处就是:(1)解题过程中较少用到空间几何中判定线线、面面、线面相对位置的有关定理,因为这些可以用向量方法来解决.(2)即使立体感稍差一些的学生也可以顺利解出,因为只需画个草图以建立坐标系和观察有关点的位置即可.
解答:(Ⅰ)证明:在正方形ADD1A1中,因为CD=AD-AB-BC=5,
所以三棱柱ABC-A1B1C1的底面三角形ABC的边AC=5.
因为AB=3,BC=4,
所以AB2+BC2=AC2,所以AB⊥BC.(2分)
因为四边形ADD1A1为正方形,AA1∥BB1,
所以AB⊥BB1,而BC∩BB1=B,
所以AB⊥平面BCC1B1.(5分)
(Ⅱ)解:因为AB⊥平面BCC1B1,
所以AB为四棱锥A-BCQP的高.
因为四边形BCQP为直角梯形,且BP=AB=3,CQ=AB+BC=7,
所以梯形BCQP的面积为SBCQP=
(BP+CQ)×BC=20.
所以四棱锥A-BCQP的体积VA-BCQP=
SBCQP×AB=20.(9分)
(Ⅲ)解:由(Ⅰ)、(Ⅱ)可知,AB,BC,BB1两两互相垂直.以B为原点,建立如图所示的空间直角坐标系B-xyz,

则A(0,0,3),B(0,0,0),C(4,0,0),P(0,3,0),Q(4,7,0),
所以
=(0,3,-3),
=(4,7,-3),
设平面PQA的一个法向量为n1=(x,y,z).
则
即
令x=-1,则y=z=1.
所以n1=(-1,1,1).(12分)
显然平面BCA的一个法向量为n2=(0,1,0).
设平面PQA与平面BCA所成锐二面角为θ.
则cosθ=cos<n1,n2>=
=
.
所以平面PQA与平面BCA所成锐二面角的余弦值为
.(14分)
所以三棱柱ABC-A1B1C1的底面三角形ABC的边AC=5.
因为AB=3,BC=4,
所以AB2+BC2=AC2,所以AB⊥BC.(2分)
因为四边形ADD1A1为正方形,AA1∥BB1,
所以AB⊥BB1,而BC∩BB1=B,
所以AB⊥平面BCC1B1.(5分)
(Ⅱ)解:因为AB⊥平面BCC1B1,
所以AB为四棱锥A-BCQP的高.
因为四边形BCQP为直角梯形,且BP=AB=3,CQ=AB+BC=7,
所以梯形BCQP的面积为SBCQP=
| 1 |
| 2 |
所以四棱锥A-BCQP的体积VA-BCQP=
| 1 |
| 3 |
(Ⅲ)解:由(Ⅰ)、(Ⅱ)可知,AB,BC,BB1两两互相垂直.以B为原点,建立如图所示的空间直角坐标系B-xyz,

则A(0,0,3),B(0,0,0),C(4,0,0),P(0,3,0),Q(4,7,0),
所以
| AP |
| AQ |
设平面PQA的一个法向量为n1=(x,y,z).
则
|
|
令x=-1,则y=z=1.
所以n1=(-1,1,1).(12分)
显然平面BCA的一个法向量为n2=(0,1,0).
设平面PQA与平面BCA所成锐二面角为θ.
则cosθ=cos<n1,n2>=
| n 1•n2 |
| |n1||n2| |
| ||
| 3 |
所以平面PQA与平面BCA所成锐二面角的余弦值为
| ||
| 3 |
点评:本小题主要考查空间线面关系、二面角的度量、几何体的体积等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
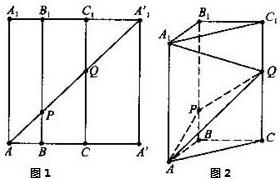 如图1所示,在边长为12的正方形AA′A′1A1中,BB1∥CC1∥AA1,且AB=3,BC=4,AA′1分别交BB1,CC1于点P、Q,将该正方形沿BB1、CC1折叠,使得A′A′1与AA1重合,构成如图2所示的三棱柱ABC-A1B1C1,请在图2中解决下列问题:
如图1所示,在边长为12的正方形AA′A′1A1中,BB1∥CC1∥AA1,且AB=3,BC=4,AA′1分别交BB1,CC1于点P、Q,将该正方形沿BB1、CC1折叠,使得A′A′1与AA1重合,构成如图2所示的三棱柱ABC-A1B1C1,请在图2中解决下列问题: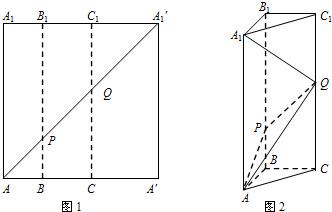 如图1所示,在边长为12的正方形AA′A1′A1中,点B,C在线段AA′上,且AB=3,BC=4,作BB1∥AA1,分别交A1A1′、AA1′于点B1、P,作CC1∥AA1,分别交A1A1′、AA1′于点C1、Q,将该正方形沿BB1、CC1折叠,使得A′A1′与AA1重合,构成如图2所示的三棱柱ABC-A1B1C1.
如图1所示,在边长为12的正方形AA′A1′A1中,点B,C在线段AA′上,且AB=3,BC=4,作BB1∥AA1,分别交A1A1′、AA1′于点B1、P,作CC1∥AA1,分别交A1A1′、AA1′于点C1、Q,将该正方形沿BB1、CC1折叠,使得A′A1′与AA1重合,构成如图2所示的三棱柱ABC-A1B1C1.
 如图1所示,在边长为
如图1所示,在边长为