摘要：知.
网址：http://m.1010jiajiao.com/timu_id_258748[举报]
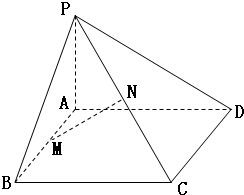已知，如图：四边形ABCD为矩形，PA⊥平面ABCD，M、N分别是AB、PC的中点，（1）求证：直线MN⊥直线AB；
（2）若平面PDC与平面ABCD所成的二面角大小为θ，能否确定θ使直线MN是异面直线AB与PC的公垂线，若能确定，求出θ的值，若不能确定，说明理由． 查看习题详情和答案>>
由于卫生的要求游泳池要经常换水（进一些干净的水同时放掉一些脏水），游泳池的水深经常变化，已知泰州某浴场的水深y（米）是时间t（0≤t≤24），（单位小时）的函数，记作y=f（t），下表是某日各时的水深数据经长期观测的曲线y=f（t）可近似地看成函数y=Acosωt+b
（Ⅰ）根据以上数据，求出函数y=Acosωt+b的最小正周期T，振幅A及函数表达式；
（Ⅱ）依据规定，当水深大于2米时才对游泳爱好者开放，请依据（1）的结论，判断一天内的上午8：00至晚上20：00之间，有多少时间可供游泳爱好者进行运动． 查看习题详情和答案>>
| t（时） | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| y（米） | 2 5 | 2 0 | 15 | 20 | 249 | 2 | 151 | 199 | 2 5 |
（Ⅱ）依据规定，当水深大于2米时才对游泳爱好者开放，请依据（1）的结论，判断一天内的上午8：00至晚上20：00之间，有多少时间可供游泳爱好者进行运动． 查看习题详情和答案>>
已知，f（x）=ax-lnx，g(x)=
，a∈R．
（1）当a=1时，讨论f（x）的单调性、极值；
（2）当a=-1时，求证：g(x2)-f(x1)＜2x1+
，?x1，x2∈(0，+∞)成立；
（3）是否存在实数a，使x∈（0，e]时，f（x）的最小值是3，若存在，求出a的值；若不存在，说明理由． 查看习题详情和答案>>
| -f(x) |
| x |
（1）当a=1时，讨论f（x）的单调性、极值；
（2）当a=-1时，求证：g(x2)-f(x1)＜2x1+
| 1 |
| 2 |
（3）是否存在实数a，使x∈（0，e]时，f（x）的最小值是3，若存在，求出a的值；若不存在，说明理由． 查看习题详情和答案>>