题目内容
 已知,如图:四边形ABCD为矩形,PA⊥平面ABCD,M、N分别是AB、PC的中点,
已知,如图:四边形ABCD为矩形,PA⊥平面ABCD,M、N分别是AB、PC的中点,(1)求证:直线MN⊥直线AB;
(2)若平面PDC与平面ABCD所成的二面角大小为θ,能否确定θ使直线MN是异面直线AB与PC的公垂线,若能确定,求出θ的值,若不能确定,说明理由.
分析:(1)由题意连接AN、BN、AC,由PA⊥面ABCD和三垂线定理得PA⊥AC、PB⊥BC,根据M、N是中点得AN=BN和MN⊥AB;
(2)假设MN是异面直线AB与PC的公垂线,得到MN⊥PC,由N是中点得CM=PM,证出△BCM≌△APM得DA=PA,根据二面角的定义和垂直关系证出∠PDA=θ,即求出此角的值.
(2)假设MN是异面直线AB与PC的公垂线,得到MN⊥PC,由N是中点得CM=PM,证出△BCM≌△APM得DA=PA,根据二面角的定义和垂直关系证出∠PDA=θ,即求出此角的值.
解答: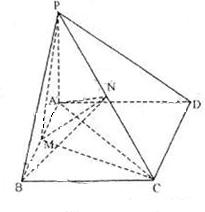 解:(1)证明:连接AN、BN、AC,
解:(1)证明:连接AN、BN、AC,
∵PA⊥面ABCD,且AC?面ABCD,
∴PA⊥AC,
∵N是PC的中点,
∴AN=
PC,
∵BC⊥AB,
∴由三垂线定理得PB⊥BC,得BN=
PC,
∴AN=BN,,∴MN⊥AB.
(2)解:假设MN是异面直线AB与PC的公垂线,则MN⊥PC,
连接CM、PM,由于N是PC的中点,∴CM=PM
∴△BCM≌△APM,∴BC=PA,∴DA=PA,
∵PA⊥面ABCD,平面ABCD是矩形,∴CD⊥面PAD,
∴PA⊥CD,AD⊥CD,
∴∠PDA为面PDC与面ABCD所成的二面角的平面角,即∠PDA=θ,
∴当θ=
时,MN为异面直线AB与PC的公垂线.
 解:(1)证明:连接AN、BN、AC,
解:(1)证明:连接AN、BN、AC,∵PA⊥面ABCD,且AC?面ABCD,
∴PA⊥AC,
∵N是PC的中点,
∴AN=
| 1 |
| 2 |
∵BC⊥AB,
∴由三垂线定理得PB⊥BC,得BN=
| 1 |
| 2 |
∴AN=BN,,∴MN⊥AB.
(2)解:假设MN是异面直线AB与PC的公垂线,则MN⊥PC,
连接CM、PM,由于N是PC的中点,∴CM=PM
∴△BCM≌△APM,∴BC=PA,∴DA=PA,
∵PA⊥面ABCD,平面ABCD是矩形,∴CD⊥面PAD,
∴PA⊥CD,AD⊥CD,
∴∠PDA为面PDC与面ABCD所成的二面角的平面角,即∠PDA=θ,
∴当θ=
| π |
| 4 |
点评:本题是关于线线(线面)垂直和二面角的综合题,主要利用等腰三角形和底边的中点和线面垂直的定义证出线线垂直,实现线线、线面垂直的相互转化,考查了推理论证和逻辑思维能力.

练习册系列答案
相关题目

 如图,四边形ABCD中,△BCD为正三角形,AD=AB=2,
如图,四边形ABCD中,△BCD为正三角形,AD=AB=2, A.已知方程|2x-1|-|2x+1|=a+1有实数解,则a的取值范围为
A.已知方程|2x-1|-|2x+1|=a+1有实数解,则a的取值范围为
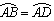 ,过A点的切线交CB的延长线于E点,求证:AB2=BE·CD。
,过A点的切线交CB的延长线于E点,求证:AB2=BE·CD。