摘要:(Ⅲ) 若对于任意的正整数.当时.都有成立,则称这样是函数.现有函数,试判断是不是函数?并给予证明.
网址:http://m.1010jiajiao.com/timu_id_250994[举报]
对于数列{xn},如果存在一个正整数m,使得对任意的n(n∈N*)都有xm+n=xn成立,那么就把这样一类数列{xn}称作周期为m的周期数列,m的最小正值称作数列{xn}的最小正周期,以下简称周期.例如当xn=2时,{xn}是周期为1的周期数列;当yn=sin(
)时,{yn}是周期为4的周期数列.设数列{an}满足an+2=λ•an+1-an(n∈N*),a1=1,a2=20.
(1)若数列{an}是周期为3的周期数列,则常数λ的值是
(2)设数列{an}的前n项和为Sn,若λ=1,则S2012=
查看习题详情和答案>>
| nπ | 2 |
(1)若数列{an}是周期为3的周期数列,则常数λ的值是
-1
-1
;(2)设数列{an}的前n项和为Sn,若λ=1,则S2012=
21
21
.对于实数x,将满足“0≤y<1且x-y为整数”的实数y称为实数x的小数部分,用记号{x}表示.例如{1.2}=0.2,{-1.2}=0.8,{
}=
.对于实数a,无穷数列{an}满足如下条件:a1={a},an+1=
其中n=1,2,3,….
(1)若a=
,求a2,a3 并猜想数列{a}的通项公式(不需要证明);
(2)当a>
时,对任意的n∈N*,都有an=a,求符合要求的实数a构成的集合A;
(3)若a是有理数,设a=
(p是整数,q是正整数,p,q互质),对于大于q的任意正整数n,是否都有an=0成立,证明你的结论.
查看习题详情和答案>>
| 8 |
| 7 |
| 1 |
| 7 |
|
(1)若a=
| 2 |
(2)当a>
| 1 |
| 4 |
(3)若a是有理数,设a=
| p |
| q |
已知函数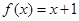 ,设
,设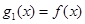 ,
,
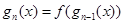
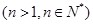 .
.
(1)猜测并直接写出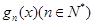 的表达式;此时若设
的表达式;此时若设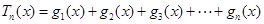 ,且关于
,且关于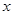 的函数
的函数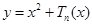
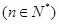 在区间
在区间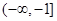 上的最小值为
上的最小值为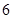 ,则求
,则求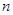 的值;
的值;
(2)设数列 为等比数列,数列
为等比数列,数列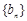 满足
满足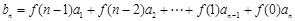 ,
,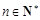 ,若
,若
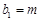 ,
,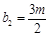 ,其中
,其中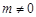 ,则
,则
①当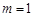 时,求
时,求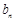 ;
;
②设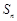 为数列
为数列 的前
的前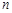 项和,若对于任意的正整数
项和,若对于任意的正整数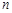 ,都有
,都有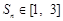 ,求实数
,求实数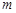 的取值范围.
的取值范围.
查看习题详情和答案>>
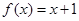 ,设
,设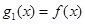 ,
,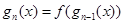
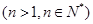 .
. 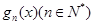 的表达式;此时若设
的表达式;此时若设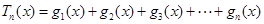 ,且关于
,且关于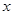 的函数
的函数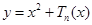
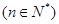 在区间
在区间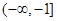 上的最小值为
上的最小值为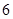 ,则求
,则求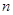 的值;
的值;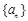 为等比数列,数列
为等比数列,数列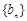 满足
满足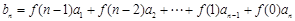 ,
,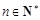 ,若
,若 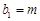 ,
,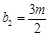 ,其中
,其中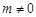 ,则
,则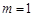 时,求
时,求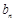 ;
;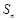 为数列
为数列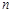 项和,若对于任意的正整数
项和,若对于任意的正整数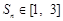 ,求实数
,求实数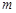 的取值范围.
的取值范围.