ĖâÄŋÄÚČÝ
ķÔÓÚĘĩĘýxĢŽ―ŦÂúŨãĄ°0ĄÜyĢž1ĮŌx-yΊÕûĘýĄąĩÄĘĩĘýyģÆΊĘĩĘýxĩÄÐĄĘýēŋ·ÖĢŽÓÞĮšÅ{x}ąíĘūĢŪĀýČį{1.2}=0.2ĢŽ{-1.2}=0.8ĢŽ{
}=
ĢŪķÔÓÚĘĩĘýaĢŽÎÞĮîĘýÁÐ{an}ÂúŨãČįÏÂĖõžþĢša1={a}ĢŽan+1=
ÆäÖÐn=1ĢŽ2ĢŽ3ĢŽĄĢŪ
ĢĻ1ĢĐČôa=
ĢŽĮóa2ĢŽa3 ēĒēÂÏëĘýÁÐ{a}ĩÄÍĻÏîđŦĘ―ĢĻēŧÐčŌŠÖĪÃũĢĐĢŧ
ĢĻ2ĢĐĩąaĢū
ĘąĢŽķÔČÎŌâĩÄnĄĘN*ĢŽķžÓÐan=aĢŽĮó·ûšÏŌŠĮóĩÄĘĩĘýađđģÉĩÄžŊšÏAĢŧ
ĢĻ3ĢĐČôaĘĮÓÐĀíĘýĢŽÉča=
ĢĻpĘĮÕûĘýĢŽqĘĮÕýÕûĘýĢŽpĢŽqŧĨÖĘĢĐĢŽķÔÓÚīóÓÚqĩÄČÎŌâÕýÕûĘýnĢŽĘĮ·ņķžÓÐan=0ģÉÁĒĢŽÖĪÃũÄãĩÄ―áÂÛĢŪ
| 8 |
| 7 |
| 1 |
| 7 |
|
ĢĻ1ĢĐČôa=
| 2 |
ĢĻ2ĢĐĩąaĢū
| 1 |
| 4 |
ĢĻ3ĢĐČôaĘĮÓÐĀíĘýĢŽÉča=
| p |
| q |
·ÖÎöĢšĢĻ1ĢĐÓÉĖâÉčÖŠa1={
}=
-1ĢŽa2={
}={
}={
+1}={
}=
-1ĢŽīÓķøŋÉēÂÏëĘýÁÐ{a}ĩÄÍĻÏîđŦĘ―Ģŧ
ĢĻ2ĢĐĩą
ĢžaĢž1ĢŽžī1Ģž
Ģž2ĘąĢŽŋÉĮóĩÃa=
ĢŽÓÉīË―øÐзÖĀāĖÖÂÛĢŽÄÜĮóģö·ûšÏŌŠĮóĩÄĘĩĘýađđģÉĩÄžŊšÏAĢŧ
ĢĻ3ĢĐģÉÁĒĢŪÖĪÃũĢšÓÉaĘĮÓÐĀíĘýĢŽŋÉÖŠķÔŌŧĮÐÕýÕûĘýnĢŽanΊ0ŧōÕýÓÐĀíĘýĢŽŋÉÉčan=
ĢŽÓÉīËĀûÓ÷ÖĀāĖÖÂÛËžÏëÄÜđŧÍÆĩžģöĘýÁÐ{am}ÖÐamŌÔž°ËüÖŪšóĩÄÏîūųΊ0ĢŽËųŌÔķÔÓÚīóÓÚqĩÄŨÔČŧĘýnĢŽķžÓÐan=0ĢŪ
| 2 |
| 2 |
| 1 |
| a1 |
| 1 | ||
|
| 2 |
| 2 |
| 2 |
ĢĻ2ĢĐĩą
| 1 |
| 2 |
| 1 |
| a |
-1+
| ||
| 2 |
ĢĻ3ĢĐģÉÁĒĢŪÖĪÃũĢšÓÉaĘĮÓÐĀíĘýĢŽŋÉÖŠķÔŌŧĮÐÕýÕûĘýnĢŽanΊ0ŧōÕýÓÐĀíĘýĢŽŋÉÉčan=
| pn |
| qn |
―âīðĢš―âĢšĢĻ1ĢĐĄßa1={
}=
-1ĢŽ
a2={
}={
}={
+1}={
}=
-1ĢŽ
ÍŽĀíŋÉĮóa3=
-1ĢŽ
ÓÚĘĮēÂÏëĢšan=
-1ĢŪ
ĢĻ2ĢĐĩą
ĢžaĢž1ĢŽžī1Ģž
Ģž2ĘąĢŽa2={
}={
}=
-1=aĢŽ
Ąāa2+a-1=0ĢŽ
―âĩÃa=
ŧōa=
ĢĻÉáČĨĢĐĢŧ
ĩą
ĢžaĄÜ
ĢŽžī2ĄÜ
Ģž3ĘąĢŽa2={
}={
}=
-2=aĢŽ
Ąāa2+2a-1=0ĢŽ
―âĩÃa=
=
-1ŧōa=-
-1ĢĻÉáČĨĢĐĢŧ
ĩą
ĢžaĄÜ
ĢŽžī3ĄÜ
Ģž4ĘąĢŽa2={
}={
}=
-3=aĢŽ
Ąāa2+3a-1=0ĢŽ
―âĩÃa=
ŧōa=
ĢĻÉáČĨĢĐĢŪ
ŨÛÉÏËųĘöĢŽ·ûšÏŌŠĮóĩÄĘĩĘýađđģÉĩÄžŊšÏA={
ĢŽ
-1ĢŽ
}ĢŪ
ĢĻ3ĢĐÓÉaĘĮÓÐĀíĘýŋÉÖŠĢŽķÔŌŧĮÐÕýÕûĘýnĢŽanΊ0ŧōÕýÓÐĀíĘýĢŪ
Éčan=
ĢĻpnĘĮ·ĮļšÕûĘýĢŽqnĘĮÕýÕûĘýĮŌ
žČÔžĢĐĢŪ
ĒŲÓÉa1={
}=
ĩÃĢš0ĄÜp1ĄÜqĢŧ
ĒÚČôpnĄŲ0ĢŽÉčqn=ĶÁpn+ĶÂĢĻ0ĄÜĶÂĢžpnĢŽĶÁĢŽĶÂΊ·ĮļšÕûĘýĢĐĢŽ
Ôō
=ĶÁ+
ĢŽķøÓÉan=
ĢŽĩÃ
=
ĢŽ
Ąāan+1={
}=
ĢŽ
Ąāpn+1=ĶÂĢŽqn+1=pnĢŽ
Ąā0ĄÜpn+1ĢžpnĢŪ
Čôpn=0ĢŽÔōpn+1=0ĢŽ
Čôa1ĄĒa2ĄĒa3ĄĒĄĄĒaqūųēŧΊ0ĢŽÔōÕâqļöÕýÕûĘýŧĨēŧÏāÍŽĮŌķžÐĄÓÚqĢŽĩŦÐĄÓÚqĩÄÕýÕûĘýđēÓÐq-1ļöĢŽÃŽķÜĢŪ
đĘa1ĄĒa2ĄĒa3ĄĒĄĄĒaqÖÐÖÁÉŲÓÐŌŧļöΊ0ĢŽžīīæÔÚmĢĻ1ĄÜmĄÜqĢĐĘđĩÃam=0ĢŪ
īÓķø{am}ÖÐamž°ŌÔšóĩÄÏîūųΊ0ĢŽËųŌÔķÔīóÓÚqĩÄČÎŌâÕýÕûĘýnĢŽķžÓÐan=0ģÉÁĒĢŽ
| 2 |
| 2 |
a2={
| 1 |
| a1 |
| 1 | ||
|
| 2 |
| 2 |
| 2 |
ÍŽĀíŋÉĮóa3=
| 2 |
ÓÚĘĮēÂÏëĢšan=
| 2 |
ĢĻ2ĢĐĩą
| 1 |
| 2 |
| 1 |
| a |
| 1 |
| a1 |
| 1 |
| a |
| 1 |
| a |
Ąāa2+a-1=0ĢŽ
―âĩÃa=
-1+
| ||
| 2 |
-1-
| ||
| 2 |
ĩą
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| a |
| 1 |
| a1 |
| 1 |
| a |
| 1 |
| a |
Ąāa2+2a-1=0ĢŽ
―âĩÃa=
-2+
| ||
| 2 |
| 2 |
| 2 |
ĩą
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| a |
| 1 |
| a1 |
| 1 |
| a |
| 1 |
| a |
Ąāa2+3a-1=0ĢŽ
―âĩÃa=
-3+
| ||
| 2 |
-3-
| ||
| 2 |
ŨÛÉÏËųĘöĢŽ·ûšÏŌŠĮóĩÄĘĩĘýađđģÉĩÄžŊšÏA={
-1+
| ||
| 2 |
| 2 |
-3+
| ||
| 2 |
ĢĻ3ĢĐÓÉaĘĮÓÐĀíĘýŋÉÖŠĢŽķÔŌŧĮÐÕýÕûĘýnĢŽanΊ0ŧōÕýÓÐĀíĘýĢŪ
Éčan=
| pn |
| qn |
| pn |
| qn |
ĒŲÓÉa1={
| p |
| q |
| p1 |
| q1 |
ĒÚČôpnĄŲ0ĢŽÉčqn=ĶÁpn+ĶÂĢĻ0ĄÜĶÂĢžpnĢŽĶÁĢŽĶÂΊ·ĮļšÕûĘýĢĐĢŽ
Ôō
| qn |
| pn |
| ĶÂ |
| pn |
| pn |
| qn |
| 1 |
| an |
| qn |
| pn |
Ąāan+1={
| 1 |
| an |
| ĶÂ |
| pn |
Ąāpn+1=ĶÂĢŽqn+1=pnĢŽ
Ąā0ĄÜpn+1ĢžpnĢŪ
Čôpn=0ĢŽÔōpn+1=0ĢŽ
Čôa1ĄĒa2ĄĒa3ĄĒĄĄĒaqūųēŧΊ0ĢŽÔōÕâqļöÕýÕûĘýŧĨēŧÏāÍŽĮŌķžÐĄÓÚqĢŽĩŦÐĄÓÚqĩÄÕýÕûĘýđēÓÐq-1ļöĢŽÃŽķÜĢŪ
đĘa1ĄĒa2ĄĒa3ĄĒĄĄĒaqÖÐÖÁÉŲÓÐŌŧļöΊ0ĢŽžīīæÔÚmĢĻ1ĄÜmĄÜqĢĐĘđĩÃam=0ĢŪ
īÓķø{am}ÖÐamž°ŌÔšóĩÄÏîūųΊ0ĢŽËųŌÔķÔīóÓÚqĩÄČÎŌâÕýÕûĘýnĢŽķžÓÐan=0ģÉÁĒĢŽ
ĩãÆĀĢšąūĖâŋžēéĘýÁÐĩÄĩÝÍÆĢŽŋžēéžŊšÏĩÄĮó·ĻĢŽŋžēéan=0ĘĮ·ņģÉÁĒĩÄÅÐķÏÓëÖĪÃũĢŪŨÛšÏÐÔĮŋĢŽžÆËãÁŋīóĢŽÄŅķČ―ÏļßĢŽķÔĘýŅ§ËžÎŽÄÜÁĶĩÄŌŠĮó―ÏļßĢŪ―âĖâĘąŌŠČÏÕæÉóĖâĢŽŨĒŌâĩČžÛŨŠŧŊËžÏëšÍ·ÖĀāĖÖÂÛËžÏëĩÄšÏĀíÔËÓÃĢŪ

Á·Ï°ēáÏĩÁÐīð°ļ
ÏāđØĖâÄŋ
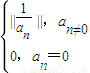 ÆäÖÐn=1ĢŽ2ĢŽ3ĢŽĄ
ÆäÖÐn=1ĢŽ2ĢŽ3ĢŽĄ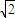 ĢŽĮóĘýÁÐ{an}Ģŧ
ĢŽĮóĘýÁÐ{an}Ģŧ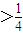 ĘąĢŽķÔČÎŌâĩÄnĄĘN*ĢŽķžÓÐan=aĢŽĮó·ûšÏŌŠĮóĩÄĘĩĘýađđģÉĩÄžŊšÏAĢŪ
ĘąĢŽķÔČÎŌâĩÄnĄĘN*ĢŽķžÓÐan=aĢŽĮó·ûšÏŌŠĮóĩÄĘĩĘýađđģÉĩÄžŊšÏAĢŪ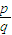 ĢĻp ĘĮÕûĘýĢŽqĘĮÕýÕûĘýĢŽpĄĒqŧĨÖĘĢĐĢŽÎĘķÔÓÚīóÓÚqĩÄČÎŌâÕýÕûĘýnĢŽĘĮ·ņķžÓÐan=0ģÉÁĒĢŽēĒÖĪÃũÄãĩÄ―áÂÛĢŪ
ĢĻp ĘĮÕûĘýĢŽqĘĮÕýÕûĘýĢŽpĄĒqŧĨÖĘĢĐĢŽÎĘķÔÓÚīóÓÚqĩÄČÎŌâÕýÕûĘýnĢŽĘĮ·ņķžÓÐan=0ģÉÁĒĢŽēĒÖĪÃũÄãĩÄ―áÂÛĢŪ