摘要:(2)问p+q是否可以是整数.若可以.当P+q为整数时.求的值,若p+q不可以为整数.说明理由.
网址:http://m.1010jiajiao.com/timu_id_25016[举报]
| |||||||||||||||||||||||||||||||||||||||||
如图,一张边长为20cm正方形硬纸板,把它的四个角都剪去一个边长为xcm的小正方形,然后把它折成一个无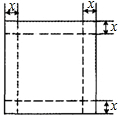 盖的长方体,设长方体的容积为Vcm3,请回答下列问题:
盖的长方体,设长方体的容积为Vcm3,请回答下列问题:
(1)若用含有x的代数式表示V,则V=
(2)根据(1)中结果,填写下表:
(3)观察(2)中表格,容积V的值是否随x值的增大而增大?此时当x取什么整数值时,容积V的值最大?
(4)课后小英同学继续对这个问题作了以下探究:
当x=3.2cm时,V=591.872cm3;当x=3.3cm时,V=592.548cm3;
当x=3.4cm时,V=592.416cm3;当x=3.5cm时,V=591.5cm3,
小英同学发现x的取值一定介于3.3cm~3.4cm之间,估计x的取值还能更精确些,小英再计算x=3.3cm,3.33cm,3.333cm,3.3333cm…时,发现容积还在逐渐增大.现请你也观察(4)中数据变化,能否推测x可以取到哪一个定值,容积V的值最大?(直接写出即可)
查看习题详情和答案>>
 盖的长方体,设长方体的容积为Vcm3,请回答下列问题:
盖的长方体,设长方体的容积为Vcm3,请回答下列问题:(1)若用含有x的代数式表示V,则V=
x(20-2x)2
x(20-2x)2
.(2)根据(1)中结果,填写下表:
| x(cm) | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| V(cm3) | 324 | 512 | 500 | 384 | 252 |
(4)课后小英同学继续对这个问题作了以下探究:
当x=3.2cm时,V=591.872cm3;当x=3.3cm时,V=592.548cm3;
当x=3.4cm时,V=592.416cm3;当x=3.5cm时,V=591.5cm3,
小英同学发现x的取值一定介于3.3cm~3.4cm之间,估计x的取值还能更精确些,小英再计算x=3.3cm,3.33cm,3.333cm,3.3333cm…时,发现容积还在逐渐增大.现请你也观察(4)中数据变化,能否推测x可以取到哪一个定值,容积V的值最大?(直接写出即可)
如图,一张边长为20cm正方形硬纸板,把它的四个角都剪去一个边长为xcm的小正方形,然后把它折成一个无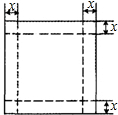 盖的长方体,设长方体的容积为Vcm3,请回答下列问题:
盖的长方体,设长方体的容积为Vcm3,请回答下列问题:
(1)若用含有x的代数式表示V,则V=______.
(2)根据(1)中结果,填写下表:
| x(cm) | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| V(cm3) | 324 | 512 | 500 | 384 | 252 |
(4)课后小英同学继续对这个问题作了以下探究:
当x=3.2cm时,V=591.872cm3;当x=3.3cm时,V=592.548cm3;
当x=3.4cm时,V=592.416cm3;当x=3.5cm时,V=591.5cm3,
小英同学发现x的取值一定介于3.3cm~3.4cm之间,估计x的取值还能更精确些,小英再计算x=3.3cm,3.33cm,3.333cm,3.3333cm…时,发现容积还在逐渐增大.现请你也观察(4)中数据变化,能否推测x可以取到哪一个定值,容积V的值最大?(直接写出即可) 查看习题详情和答案>>
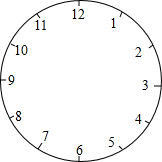 钟面数字问题
钟面数字问题如图,钟面上有1,2,3,…,11,12这12个数字.
(1)试在某些数的前面添加负号,使它们的代数和为零
(2)能否改变钟面上的数,比如只剩下6个偶数,仍按第(1)小题的要求来做?
[思路探究]
(1)我们先试着选定任意几个数字,在其前面添加负号,如
-12-11-10+9+8+7+6-5+4+3+2+1-2.
这当然不是我们要的答案,但我们可以将其调整,比如改变1前面的符号,得
-12-11-10+9+8+7+6-5+4+3+2-1-0.
用这种方法当然可以得到许多答案,但我们并不满足.我们希望寻找其中的规律,使我们能找到更多的解答.我们发现:
在调整符号的过程中,若将一个正数变号,12个数的代数和就减少这个正数的两倍;若将一个负数变号,12个数的代数和就增加这个负数的绝对值的两倍.
要使12个数的代数和为零,其中正数的和的绝对值必须与负数的和的绝对值相等,均为12个数之和的-半,即等于39.
由此,我们只要找到几个和为39的数,将这些数添上负号即可.
由于最大3个数之和为33<39,因此必须再添上一个6才有解答,所以添加负号的数至少要有4个.同理可知,添加负号的数最多不超过8个.
根据以上规律,就能在很短的时间内得到许多解答,但是要写出所有解答,还必须把答案作适当的分类.本题共有124个解答,亲爱的读者,你能写出这124个解答来吗?
(2)因为2+4+6+8+10+12-42,它的一半为21,而奇数不可能通过偶数求和得到,所以只剩下6个偶数时,不能按第(1)小题的要求来做.
 钟面数字问题
钟面数字问题