网址:http://m.1010jiajiao.com/timu_id_24528[举报]
一、选择题
题号
1
2
3
4
5
6
7
8
9
10
11
12
选项
A
B
B
D
B
D
C
A
B
C
A
D
二、填空题
13、(-¥,-1)È(2,+¥) 14 、2n ?
1 15、45 16、 17、0.94 18、
17、0.94 18、
三、解答题
19、解: 设等比数列{an}的公比为q, 则q≠0, a2= = , a4=a3q=2q
所以 + 2q= , 解得q1= , q2= 3,
当q1=, a1=18.所以 an=18×()n-1= = 2×33-n.
当q=3时, a1= , 所以an=×3n-1=2×3n-3
 20、解:(1)将函数解析式变形为
20、解:(1)将函数解析式变形为


 (2)方程f(x)=5的解分别是
和 , 由于f(x)在(-∞,-1]和[2,5]上单调递减,在[-1,2]和[5,+∞)上单调递增,因此
(2)方程f(x)=5的解分别是
和 , 由于f(x)在(-∞,-1]和[2,5]上单调递减,在[-1,2]和[5,+∞)上单调递增,因此
 .
.
 由于
由于
21、解:(1)当a=2时,A=(2,7),B=(4,5)∴ A B=(4,5)
B=(4,5)
(2)∵ B=(
当a< 时,A=(
时,A=( A,必须
A,必须 ,此时a=-1;
,此时a=-1;
当a= 时,A=
时,A= ,使B
,使B A的a不存在;
A的a不存在;
当a> 时,A=(2,
时,A=(2, A,必须
A,必须 ,此时1≤a≤3.
,此时1≤a≤3.
综上可知,使B A的实数a的取值范围为[1,3]∪{-1}
A的实数a的取值范围为[1,3]∪{-1}
22、解:(Ⅰ)求导得 。
。
由于  的图像与直线
的图像与直线 相切于点
相切于点 ,
,
所以 ,即:
,即:
 1
1 .
.
3
(Ⅱ)由 得:
得:
令f′(x)>0,解得 x<-1或x>3;又令f′(x)< 0,解得 -1<x<3.
故当x (
( , -1)时,f(x)是增函数,当 x
, -1)时,f(x)是增函数,当 x (3,
(3, )时,f(x)也是增函数,
)时,f(x)也是增函数,
但当x (-1 ,3)时,f(x)是减函数.
(-1 ,3)时,f(x)是减函数.
表1
| 生产能力分组 | [110,120) | [120,130) | [130,140) | [140,150) |
| 人数 | 8 | x | 3 | 2 |
| 生产能力分组 | [110,120) | [120,130) | [130,140) | [140,150) |
| 人数 | 6 | y | 27 | 18 |

(Ⅱ)完成下面2×2列联表,并回答能否有99.9%的把握认为“工人的生产能力与工人的类别有关”?
| 生产能力分组 | [110,130) | [130,150) | 合计 |
| A类工人 | |||
| B类工人 | |||
| 合计 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| P(K2≥k) | 0,05 | 0.025 | 0.01 | 0.005 |
| k | 3.841 | 5.024 | 6.635 | 7.879 |
(2012•武昌区模拟)通过随机询问110名性别不同的行人,对过马路是愿意走斑马线还是愿意走人行天桥进行抽样调查,得到如下的列联表:
参照独立性检验附表,得到的正确结论是( ) |
| a |
| b |
| c |
| d |
| 1 |
| 2 |
(1)若θ∈(0,
| π |
| 4 |
| a |
| b |
| c |
| d |
(2)若θ∈[0,π),函数f(x)=|x-1|,比较f(
| a |
| b |
| c |
| d |
| 男性 | 女性 | 合计 | |
| 反感 | 10 | ||
| 不反感 | 8 | ||
| 合计 | 30 |
| 8 |
| 15 |
(Ⅰ)请将上面的列表补充完整(在答题卡上直接填写结果,不需要写求解过程),并据此资料分析反感“中国式过马路”与性别是否有关?(x2=
| (a+b+c+d)(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
(Ⅱ)若从这30人中的女性路人中随机抽取2人参加一活动,记反感“中国式过马路”的人数为X,求X的分布列和数学期望.
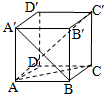 如图,在正方体ABCD-A′B′C′D′中,直线A′B和直线AC、CC′、C′A所成的角的大小分别是α、β、γ,则α、β、γ的大小关系是( )
如图,在正方体ABCD-A′B′C′D′中,直线A′B和直线AC、CC′、C′A所成的角的大小分别是α、β、γ,则α、β、γ的大小关系是( )