题目内容
某工厂有工人1000名,其中250名工人参加过短期培训(称为A类工人)另外750名工人参加过长期培训(称为B类工人).现用分层抽样的方法(按A类、B类分两层)从该工厂的工人中抽取100名工人,调查他们的生产能力(此处生产能力指一天加工的零件数).从A类工人中的抽查结果和从B类工人中的抽查结果如下表1和表2.
表1
表2
(Ⅰ)先确定x、y的值,再补齐下列频率分布直方图.

(Ⅱ)完成下面2×2列联表,并回答能否有99.9%的把握认为“工人的生产能力与工人的类别有关”?
附:K2=
表1
| 生产能力分组 | [110,120) | [120,130) | [130,140) | [140,150) |
| 人数 | 8 | x | 3 | 2 |
| 生产能力分组 | [110,120) | [120,130) | [130,140) | [140,150) |
| 人数 | 6 | y | 27 | 18 |

(Ⅱ)完成下面2×2列联表,并回答能否有99.9%的把握认为“工人的生产能力与工人的类别有关”?
| 生产能力分组 | [110,130) | [130,150) | 合计 |
| A类工人 | |||
| B类工人 | |||
| 合计 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| P(K2≥k) | 0,05 | 0.025 | 0.01 | 0.005 |
| k | 3.841 | 5.024 | 6.635 | 7.879 |
分析:(I)根据总体数和样本容量,得到每个个体被抽到的概率,得到两个组各自需要抽取的人数,减去已知的人数,得到x,y的值,根据所给的两个频率分布表做出频率分布直方图.
(II)先根据所给的数据得到列联表,把列联表中的数据代入求观测值的公式,求出这组数据的观测值,把观测值同临界值表中的数据进行比较得到对应的概率的值,得到有99.9%的把握认为“工人的生产能力与工人的类别有关”
(II)先根据所给的数据得到列联表,把列联表中的数据代入求观测值的公式,求出这组数据的观测值,把观测值同临界值表中的数据进行比较得到对应的概率的值,得到有99.9%的把握认为“工人的生产能力与工人的类别有关”
解答:解:(Ⅰ)∵从该工厂的工人中抽取100名工人,其中250名A类工人,另外750名B类工人,
∴要从A类工人中抽取25个人,从B类工人中抽取75个人,
∴x=25-8-3-2=12,y=75-6-27-18=24
∴频率分布直方图是:

(II)根据所给的数据可以得到列联表:
把列联表中的数据代入求观测值的公式得到K2=
=12.
由于K2>10.828,
所以有99.9%的把握认为“工人的生产能力与工人的类别有关”.
∴要从A类工人中抽取25个人,从B类工人中抽取75个人,
∴x=25-8-3-2=12,y=75-6-27-18=24
∴频率分布直方图是:

(II)根据所给的数据可以得到列联表:
| 生产能力分组 | [110,130) | [130,150) | 合计 |
| A类工人 | 20 | 5 | 25 |
| B类工人 | 30 | 45 | 75 |
| 合计 | 50 | 50 | 100 |
| 100(900-150)2 |
| 50×50×25×75 |
由于K2>10.828,
所以有99.9%的把握认为“工人的生产能力与工人的类别有关”.
点评:本题考查频率分布直方图,考查独立性检验的应用,考查分层抽样,本题解题的关键是根据根据分层抽样做出两个数值,再进行下面的画图和列表,本题是一个中档题目.

练习册系列答案
相关题目
某工厂有工人1000名,其中250名工人参加过短期培训(称为A类工人),另外750名工人参加过长期培训(称为B类工人),现用分层抽样方法(按A类、B类分二层)从该工厂的工人中共抽查100名工人,调查他们的生产能力(此处生产能力指一天加工的零件数).
(I)求甲、乙两工人都被抽到的概率,其中甲为A类工人,乙为B类工人;
(II)从A类工人中的抽查结果和从B类工人中的抽插结果分别如下表1和表2.
表1:
表2:
(i)先确定x,y,再在答题纸上完成下列频率分布直方图.就生产能力而言,A类工人中个体间的差异程度与B类工人中个体间的差异程度哪个更小?(不用计算,可通过观察直方图直接回答结论)
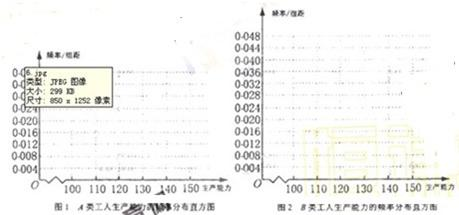
(ii)分别估计A类工人和B类工人生产能力的平均数,并估计该工厂工人的生产能力的平均数,同一组中的数据用该组区间的中点值作代表)
(I)求甲、乙两工人都被抽到的概率,其中甲为A类工人,乙为B类工人;
(II)从A类工人中的抽查结果和从B类工人中的抽插结果分别如下表1和表2.
表1:
| 生产能力分组 | [100,110] | [110,120] | [120,130] | [130,140] | [140,150] |
| 人数 | 4 | 8 | x | 5 | 3 |
| 生产能力分组 | [110,120] | [120,130] | [130,140] | [140,150] |
| 人数 | 6 | y | 36 | 18 |

(ii)分别估计A类工人和B类工人生产能力的平均数,并估计该工厂工人的生产能力的平均数,同一组中的数据用该组区间的中点值作代表)




