网址:http://m.1010jiajiao.com/timu_id_217821[举报]
一、选择题(本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中,只有一项是符合题目要求的)
题号
1
2
3
4
5
6
7
8
9
10
答案
D
C
B
B
C
A
D
B
A
C
 二、填空题(每小题4分,共28分)
二、填空题(每小题4分,共28分)
11.1+2i
12.5
13.  14. 13
14. 13
15. 2或 16.
16.  17.9
17.9
三、解答题:本大题共5小题,满分72分.解答须写出文字说明、证明过程和演算步骤.
18.(本题满分14分)
解:(1)f(x)= T=4
T=4
(2) (3)
(3) 两边平方得
两边平方得
 ,而
,而 ∴
∴
 19.(本小题满分14分)
19.(本小题满分14分)
(1)证明:∵A/O⊥面CEFB
∴EF⊥A/O,又EF⊥EC
A/O∩EC=0
∴EF⊥面A/EC
而A/C 面A/EC
面A/EC
∴EF⊥A/C
(2)
20.(本题满分14分)
解:(1)an+1=2Sn+1,an=2Sn-1+1两式相减得an+1=3an(a≥2),又a2=2S1+1=
∴ {an}是以a1=1为首项,3为公比的等比数列,an=3n-1
{an}是以a1=1为首项,3为公比的等比数列,an=3n-1
(2)Tn= 5n2+20n
5n2+20n
21.(本小题满分15分)
解:(1)W:x2=6y
(2)设AC:
设A(x1,y1),C(x2,y2) |AC|=6(k2+1)
同理|BD|=6
SABCD=
当k=±1时取等号
22.(本小题满分15分)
解:(1)f(x)=ax3 4ax2+4ax
4ax2+4ax
f/(x)=3ax2 8ax+
8ax+ 2)(x
2)(x 2)=0
2)=0 x=
x= 或2
或2
∵f(x)有极大值32,而f(2)=0
∴f( )=32=7,a=27
)=32=7,a=27
(2)f/(x)=a(3x 2)(x
2)(x 2)
2)
当a>0时,f(x)=[  2,
2, ]上递增在[
]上递增在[ ]上递减,
]上递减,
 ∴0<a<
∴0<a<
当a<0时,f(x)在[ 2,
2, ]上递减,在[
]上递减,在[ ]上递增
]上递增
f( 2)=
2)= 
 ∴
∴
综上
 ;
;(Ⅱ)利用第(Ⅰ)问的结果证明Cn1+2Cn2+3Cn3+…+nCnn=n•2n-1;
(Ⅲ)其实我们常借用构造等式,对同一个量算两次的方法来证明组合等式,譬如:(1+x)1+(1+x)2+(1+x)3+…+(1+x)n=
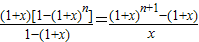 ;,由左边可求得x2的系数为C22+C32+C42+…+Cn2,利用右式可得x2的系数为Cn+13,所以C22+C32+C42+…+Cn2=Cn+13.请利用此方法证明:(C2n)2-(C2n1)2+(C2n2)2-(C2n3)2+…+(C2n2n)2=(-1)nC2nn.
;,由左边可求得x2的系数为C22+C32+C42+…+Cn2,利用右式可得x2的系数为Cn+13,所以C22+C32+C42+…+Cn2=Cn+13.请利用此方法证明:(C2n)2-(C2n1)2+(C2n2)2-(C2n3)2+…+(C2n2n)2=(-1)nC2nn.查看习题详情和答案>>
| sinx |
| 1-cosx |
| 1+cosx |
| sinx |
(Ⅱ)化简:
| tan(3π-α) | ||
sin(π-α)sin(
|
sin(2π-α)cos(α-
| ||
sin(
|
| C | m n |
| n |
| m |
| C | m-1 n-1 |
(Ⅱ)利用第(Ⅰ)问的结果证明Cn1+2Cn2+3Cn3+…+nCnn=n•2n-1;
(Ⅲ)其实我们常借用构造等式,对同一个量算两次的方法来证明组合等式,譬如:(1+x)1+(1+x)2+(1+x)3+…+(1+x)n=
| (1+x)[1-(1+x)n] |
| 1-(1+x) |
| (1+x)n+1-(1+x) |
| x |
 ;
; .
.