题目内容
(Ⅰ)求证:
=
;
(Ⅱ)利用第(Ⅰ)问的结果证明Cn1+2Cn2+3Cn3+…+nCnn=n•2n-1;
(Ⅲ)其实我们常借用构造等式,对同一个量算两次的方法来证明组合等式,譬如:(1+x)1+(1+x)2+(1+x)3+…+(1+x)n=
=
;,由左边可求得x2的系数为C22+C32+C42+…+Cn2,利用右式可得x2的系数为Cn+13,所以C22+C32+C42+…+Cn2=Cn+13.请利用此方法证明:(C2n0)2-(C2n1)2+(C2n2)2-(C2n3)2+…+(C2n2n)2=(-1)nC2nn.
| C | m n |
| n |
| m |
| C | m-1 n-1 |
(Ⅱ)利用第(Ⅰ)问的结果证明Cn1+2Cn2+3Cn3+…+nCnn=n•2n-1;
(Ⅲ)其实我们常借用构造等式,对同一个量算两次的方法来证明组合等式,譬如:(1+x)1+(1+x)2+(1+x)3+…+(1+x)n=
| (1+x)[1-(1+x)n] |
| 1-(1+x) |
| (1+x)n+1-(1+x) |
| x |
分析:(Ⅰ)分析右式,将组合数公式展开,可得
=
,利用组合数可得与左式相等,即可证明原式,
(Ⅱ)由(Ⅰ)可得:mCnm=nCn-1m-1,则左式可以变形为nCn-10+nCn-11+nCn-12+…+nCn-1n-1,进而可以变为n(Cn-10+nCn-11+nCn-12+…+nCn-1n-1),由二项式系数的性质,可变形为n•2n-1,即可证明原式;
(Ⅲ)根据题意,构造等式(x-1)2n•(x+1)2n=(x2-1)2n,分别从左式和右式求得x2n的系数,令其相等,即可证明原式.
| n |
| m |
| (n-1)! |
| (m-1)![(n-1)-(m-1)]! |
| n! |
| m!(n-m)! |
(Ⅱ)由(Ⅰ)可得:mCnm=nCn-1m-1,则左式可以变形为nCn-10+nCn-11+nCn-12+…+nCn-1n-1,进而可以变为n(Cn-10+nCn-11+nCn-12+…+nCn-1n-1),由二项式系数的性质,可变形为n•2n-1,即可证明原式;
(Ⅲ)根据题意,构造等式(x-1)2n•(x+1)2n=(x2-1)2n,分别从左式和右式求得x2n的系数,令其相等,即可证明原式.
解答:证明:(Ⅰ)右式=
=
=Cnm=左式,
原等式可得证明;
(Ⅱ)由(Ⅰ)可得:mCnm=nCn-1m-1,
故左式=nCn-10+nCn-11+nCn-12+…+nCn-1n-1=n(Cn-10+nCn-11+nCn-12+…+nCn-1n-1)=n•2n-1;
原等式可得证明;
(Ⅲ)根据题意,构造等式(x-1)2n•(x+1)2n=(x2-1)2n,
由左式可得x2n的系数为C2n2n•(-1)2nC2n0+C2n2n-1•(-1)2n-1C2n1+C2n2n-2•(-1)2n-2C2n2+…+C2n0•(-1)0C2n2n,
即(C2n0)2-(C2n1)2+(C2n2)2-(C2n3)2+…+(C2n2n)2,
由右式可得得x2n的系数为(-1)nC2nn,
故有(C2n0)2-(C2n1)2+(C2n2)2-(C2n3)2+…+(C2n2n)2=(-1)nC2nn,
原等式可得证明.
| n |
| m |
| (n-1)! |
| (m-1)![(n-1)-(m-1)]! |
| n! |
| m!(n-m)! |
原等式可得证明;
(Ⅱ)由(Ⅰ)可得:mCnm=nCn-1m-1,
故左式=nCn-10+nCn-11+nCn-12+…+nCn-1n-1=n(Cn-10+nCn-11+nCn-12+…+nCn-1n-1)=n•2n-1;
原等式可得证明;
(Ⅲ)根据题意,构造等式(x-1)2n•(x+1)2n=(x2-1)2n,
由左式可得x2n的系数为C2n2n•(-1)2nC2n0+C2n2n-1•(-1)2n-1C2n1+C2n2n-2•(-1)2n-2C2n2+…+C2n0•(-1)0C2n2n,
即(C2n0)2-(C2n1)2+(C2n2)2-(C2n3)2+…+(C2n2n)2,
由右式可得得x2n的系数为(-1)nC2nn,
故有(C2n0)2-(C2n1)2+(C2n2)2-(C2n3)2+…+(C2n2n)2=(-1)nC2nn,
原等式可得证明.
点评:本题考查组合数公式的应用,涉及二项式定理的应用,关键要根据题意,充分利用组合数的性质.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
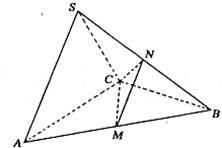 如图,三棱锥S-ABC中,△ABC是边长为4的正三角形,
如图,三棱锥S-ABC中,△ABC是边长为4的正三角形, 已知四棱锥P-ABCD的底面ABCD为平行四边形,M,N分别是棱AB,PC的中点,平面CMN与平面PAD交于PE,求证:
已知四棱锥P-ABCD的底面ABCD为平行四边形,M,N分别是棱AB,PC的中点,平面CMN与平面PAD交于PE,求证: