题目内容
(Ⅰ)求证: ;
;(Ⅱ)化简:
 .
.
【答案】分析:(Ⅰ)(法一)由比例性质(1-cosx)•(1+cosx)=1-cos2x=sin2x可证;
(法二)利用sin2x+cos2x=1,移项整理即可;
(法三)作差整理,最后证得差为0即可.
(Ⅱ)利用诱导公式与三角函数间的关系式即可证得结论.
解答:(Ⅰ)证明:(法一)利用比例性质
∵(1-cosx)•(1+cosx)=1-cos2x=sin2x
∴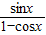 =
=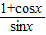 …(5分)
…(5分)
(法二)
∵sin2x+cos2x=1,
∴1-cos2x=sinx•sinx,即(1-cosx)•(1+cosx)=sinx•sinx
又∵(1-cosx)≠0,sinx≠0
∴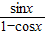 =
=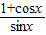 …(5分)
…(5分)
(法三)
∵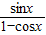 -
-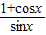
=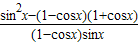
=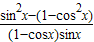
=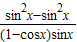 =0
=0
∴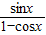 =
=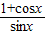 …(5分)
…(5分)
(Ⅱ)原式=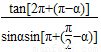 +
+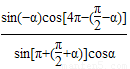
=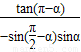 +
+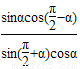
=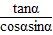 -
-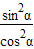
=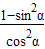 =
=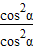 =1.…(12分)
=1.…(12分)
点评:本题考查三角函数恒等式的证明,着重考查诱导公式与同角三角函数间的基本关系,考查三角函数的化简求值,属于中档题.
(法二)利用sin2x+cos2x=1,移项整理即可;
(法三)作差整理,最后证得差为0即可.
(Ⅱ)利用诱导公式与三角函数间的关系式即可证得结论.
解答:(Ⅰ)证明:(法一)利用比例性质
∵(1-cosx)•(1+cosx)=1-cos2x=sin2x
∴
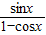 =
=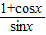 …(5分)
…(5分)(法二)
∵sin2x+cos2x=1,
∴1-cos2x=sinx•sinx,即(1-cosx)•(1+cosx)=sinx•sinx
又∵(1-cosx)≠0,sinx≠0
∴
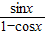 =
=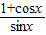 …(5分)
…(5分)(法三)
∵
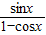 -
-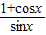
=
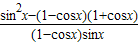
=
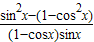
=
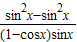 =0
=0∴
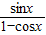 =
=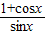 …(5分)
…(5分)(Ⅱ)原式=
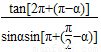 +
+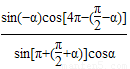
=
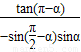 +
+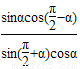
=
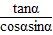 -
-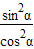
=
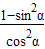 =
=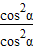 =1.…(12分)
=1.…(12分)点评:本题考查三角函数恒等式的证明,着重考查诱导公式与同角三角函数间的基本关系,考查三角函数的化简求值,属于中档题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目