摘要：(Ⅱ)∵PO⊥平面ABF.∴平面PBF⊥平面ABC,而O为BF中点.ABCDEF是正六边形 .∴A.O.D共线.且直线AD⊥BF.则AD⊥平面PBF,又∵正六边形ABCDEF的边长为1.∴AO＝.AO＝.BO＝.过O在平面POB内作OH⊥PB于H.连AH.DH.则AH⊥PB.DH⊥PB.所以∠AHD为所求二面角平面角.
网址：http://m.1010jiajiao.com/timu_id_21160[举报]
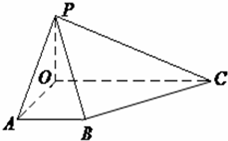如图，在四棱锥P-ABCO中，底面四边形OABC是直角梯形，∠AOC=90°，AB∥OC，PO⊥平面OABC，且|OC|=3a，|PO|=|AO|=|AB|=a．（1）求证：AO⊥平面POC；
（2）求异面直线PA与BC所成角的大小． 查看习题详情和答案>>
在四棱锥P-ABCD中，底面ABCD是边长为
的菱形，AC与BD交于O，PO⊥平面ABCD，PA=
，则PB长度的取值范围为（ ）
| 3 |
| 5 |
A、(
| ||||||||
B、(
| ||||||||
C、(
| ||||||||
D、(
|
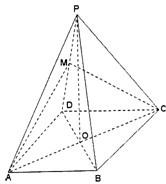如图，在四棱锥P-ABCD中，底面ABCD为等腰梯形，AB∥CD，AD=BC=2，对角线AC⊥BD于O，∠DAO=60°，且PO⊥平面ABCD，直线PA与底面ABCD所成的角为60°，M为PD上的一点．（Ⅰ）证明：PD⊥AC；
（Ⅱ）求二面角A-PB-D的大小． 查看习题详情和答案>>
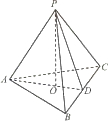如图，在三棱锥P-ABC中，AB=AC，D为BC的中点，PO⊥平面ABC，垂足O落在线段AD上，已知BC=8，PO=4，AO=3，OD=2
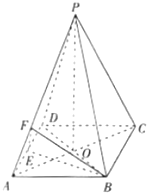如图，已知四棱锥P-ABCD的底面积是菱形，AC交BD于O，PO⊥平面ABC，E为AD中点，F在PA上，AP=λAF，PC∥平面BEF．