摘要：＜em＜ ①
网址：http://m.1010jiajiao.com/timu_id_20552[举报]
函数f（x）=
x2-2tx+3lnx，g（x）=
，函数f（x）在x=a，x=b处取得极值（0＜a＜b），g（x）在[-b，-a]上的最大值比最小值大
，若方程f（x）=m有3个不同的解，则函数y=em+
的值域为
查看习题详情和答案>>
| 1 |
| 2 |
| x+t |
| x2+3 |
| 1 |
| 3 |
| 15 |
| 2 |
（27，e4）．
（27，e4）．
．如图，在正四棱柱ABCD－A1B1C1D1中AA1＝
AB．点E、M分别为A1B1、C1C的中点，过点A1，B、M的平面交C1D1于N
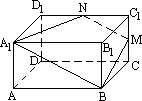
(1)求证EM∥平面A1B1C1D1．
(2)求二面角B－A1N－B1的正切值
(3)设截面A1BMN把该正四棱柱截成的两个几何体的体积为V1，V2(V1＜V2)，求V1∶V2的值．
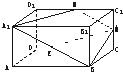如图，在正四棱柱ABCD-A1B1C1D1中，AA1=| 1 | 2 |
（1）求证：EM∥平面A1B1C1D1；
（2）求二面角B-A1N-B1的正切值；
（3）设截面A1BMN把该正四棱柱截成的两个几何体的体积分别为V1、V2（V1＜V2），求V1：V2的值． 查看习题详情和答案>>
AB，点E、M分别为A1B、C1C的中点，过点A1、B、M三点的平面A1BMN交C1D1于点N．
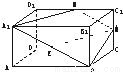
如图，已知|AB|=10，图中的一系列圆是圆心分别为A、B的两组同心圆，每组同心圆的半径分别是1，2，3，…，n，…．利用这两组同心圆可以画出以A、B为焦点的双曲线．若其中经过点M、N、P的双曲线的离心率分别是eM，eN，eP．则它们的大小关系是