Question

如图，在正四棱柱ABCD－A₁B₁C₁D₁中AA₁＝AB．点E、M分别为A₁B₁、C₁C的中点，过点A₁，B、M的平面交C₁D₁于N

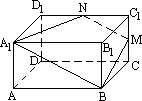
(1)求证EM∥平面A₁B₁C₁D₁．

(2)求二面角B－A₁N－B₁的正切值

(3)设截面A₁BMN把该正四棱柱截成的两个几何体的体积为V₁，V₂(V₁＜V₂)，求V₁∶V₂的值．

Answer 1

答案：
解析：

(1)易证NMA1E 　　∴四边形A1EMN为． 　　∴ME∥A1N 　　∴ME∥平面A1B1C1D1． 　　(2)连B1N，易知B1N⊥A1N，B1N为BN在上底面射影． 　　∴BN⊥A1N，则∠BNB1为所求，易知tanBNB1＝ 　　(3)延长A1N，B1C，BM，则三者交于一点P，且易知B1C1＝C1P． 　　∵平面MNC1∥平面BA1B1 　　∴几何体MNC1－BA1B1为棱台．＝()3＝，Vp－A1B1B＝×·2a·a·2a＝a3 　　∴VNC1M－A1B1B＝×a3＝a3 　　∴V1＝a3，V正面体＝2a3，V2＝(2－)a3＝a3，V1∶V2＝7∶17