摘要：l:x=2的距离之比为, (1)求双曲线的标准方程 (2)设过点F的直线交动点M的轨迹于A.B两点.且线段AB中点在直线x+y=0上. 求AB的方程. 参 考 答 案 一.ADDBC ADBCB AC二.
网址：http://m.1010jiajiao.com/timu_id_205197[举报]
以下五个关于圆锥曲线的命题中：
①平面内到定点A（1，0）和定直线l：x=2的距离之比为
的点的轨迹方程是
+
=1；
②点P是抛物线y2=2x上的动点，点P在y轴上的射影是M点A的坐标是A（3，6），则|PA|+|PM|的最小值是6；
③平面内到两定点距离之比等于常数λ（λ＞0）的点的轨迹是圆；
④若动点M（x，y）满足
=|2x-y-4|，则动点M的轨迹是双曲线；
⑤若过点C（1，1）的直线l交椭圆
+
=1于不同的两点A，B，且C是AB的中点，则直线l的方程是3x+4y-7=0．
其中真命题的序号是 ．（写出所有真命题的序号）
查看习题详情和答案>>
①平面内到定点A（1，0）和定直线l：x=2的距离之比为
| 1 |
| 2 |
| x2 |
| 4 |
| y2 |
| 3 |
②点P是抛物线y2=2x上的动点，点P在y轴上的射影是M点A的坐标是A（3，6），则|PA|+|PM|的最小值是6；
③平面内到两定点距离之比等于常数λ（λ＞0）的点的轨迹是圆；
④若动点M（x，y）满足
| (x-1)2+(y+2)2 |
⑤若过点C（1，1）的直线l交椭圆
| x2 |
| 4 |
| y2 |
| 3 |
其中真命题的序号是
（12分）已知动点P到定点F (
, 0 ) 的距离与点 P 到定直线 l：x＝2 的距离之比为
。
（1）求动点P的轨迹C的方程；
（2）设M、N是直线l上的两个点，点E是点F关于原点的对称点，若
·
＝0，
求 | MN | 的最小值。
查看习题详情和答案>>
（12分）已知动点P到定点F (
, 0 ) 的距离与点 P 到定直线 l：x＝2 的距离之比为
。
（1）求动点P的轨迹C的方程；
（2）设M、N是直线l上的两个点，点E是点F关于原点的对称点，若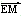
·
＝0，
求 | MN | 的最小值。
查看习题详情和答案>>
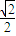，一条准线的方程是x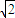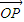=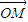2
=
+2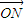
，其中M、N是椭圆上的点，直线OM与ON的斜率之积为-
，
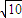的距离之比为定值；若存在，求F的坐标，若不存在，说明理由．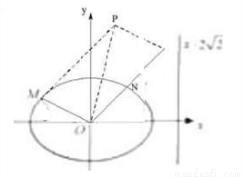
的点的轨迹方程是
；
，则动点M的轨迹是双曲线；
于不同的两点A，B，且C是AB的中点，则直线l的方程是3x+4y-7=0．