题目内容
(12分)已知动点P到定点F ( , 0 ) 的距离与点 P 到定直线 l:x=2
, 0 ) 的距离与点 P 到定直线 l:x=2 的距离之比为
的距离之比为 。
。
(1)求动点P的轨迹C的方程;
(2)设M、N是直线l上的两个点,点E是点F关于原点的对称点,若 ·
· =0,
=0,
求 | MN | 的最小值。

【答案】
(1)设点P(x,y)
依题意,有 =
=
整理得: = 1
= 1
所以动点P的轨迹方程为 +
+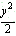 =1
=1
(2)∵点E与点F关于原点对称
∴E(- ,0)
,0)
∵M、N是l上的两点
∴可设M(2 ,y1) N(2
,y1) N(2 ,y2)
,y2)
(不妨设,y1>y2)
∵ ·
· =0
=0
∴(3 ,y1)·(
,y1)·( ,y2)=0
,y2)=0
即6 + y1y2=0
∴y2=-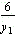
由于y1>y2,∴y1>0,y2<0
∴| MN |=y1-y2=y1 +  ≥2
≥2 =2
=2
当且仅当y1= ,y2=-
,y2=- 时,取“=”号,故| MN |的最小值为2
时,取“=”号,故| MN |的最小值为2
【解析】略

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
 , 0 ) 的距离与点 P 到定直线 l:x=2
, 0 ) 的距离与点 P 到定直线 l:x=2 。
。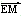 ·
· =0,
=0,