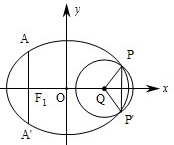
题目内容
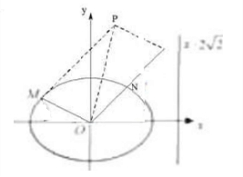
如图,椭圆的中心为原点0,离心率e=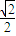 ,一条准线的方程是x=2
,一条准线的方程是x=2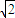
(Ⅰ)求椭圆的标准方程;
(Ⅱ)设动点P满足:
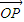 =
=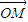 +2
+2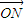 ,其中M、N是椭圆上的点,直线OM与ON的斜率之积为-
,其中M、N是椭圆上的点,直线OM与ON的斜率之积为- ,
,问:是否存在定点F,使得|PF|与点P到直线l:x=2
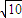 的距离之比为定值;若存在,求F的坐标,若不存在,说明理由.
的距离之比为定值;若存在,求F的坐标,若不存在,说明理由.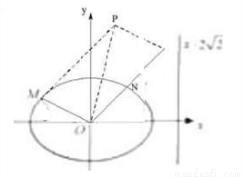
【答案】分析:(Ⅰ) 由题意得 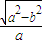 =
=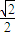 ,
,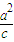 =
=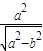 =2
=2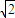 ,解出a、b 的值,即得椭圆的标准方程.
,解出a、b 的值,即得椭圆的标准方程.
(Ⅱ)设动点P(x,y),M(x1,y1 )、N(x2,y2 ). 由向量间的关系得到 x=x1+2x2,y=y1+2y2,据M、N是椭圆上的点可得 x2+2y2=20+4(x1x2+2y1y2 ).再根据直线OM与ON的斜率之积为- ,得到点P是椭圆 x2+2y2=20 上的点,根据椭圆的第二定义,存在点F(
,得到点P是椭圆 x2+2y2=20 上的点,根据椭圆的第二定义,存在点F(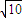 ,0),满足条件.
,0),满足条件.
解答:解:(Ⅰ) 由题意得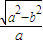 =
=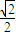 ,
,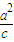 =
=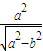 =2
=2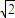 ,∴a=2,b=
,∴a=2,b=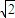 ,
,
故椭圆的标准方程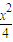 +
+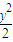 =1.
=1.
(Ⅱ)设动点P(x,y),M(x1,y1 )、N(x2,y2 ).∵动点P满足: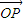 =
=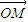 +2
+2 ,
,
∴(x,y)=(x1+2x2,y1+2y2 ),∴x=x1+2x2,y=y1+2y2,
∵M、N是椭圆上的点,∴x12+2y12-4=0,x22+2y22-4=0.
∴x2+2y2=(x1+2x2)2+2 (y1+2y2)2=(x12+2y12 )+4(x22+2y22 )+4(x1x2+2y1y2 )
=4+4×4+4(x1x2+2y1y2 )=20+4(x1x2+2y1y2 ).
∵直线OM与ON的斜率之积为- ,∴
,∴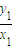 •
•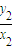 =-
=- ,∴x2+2y2=20,
,∴x2+2y2=20,
故点P是椭圆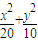 =1 上的点,焦点F(
=1 上的点,焦点F(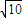 ,0),准线l:x=2
,0),准线l:x=2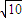 ,离心率为
,离心率为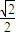 ,
,
根据椭圆的第二定义,|PF|与点P到直线l:x=2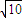 的距离之比为定值
的距离之比为定值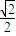 ,
,
故存在点F(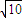 ,0),满足|PF|与点P到直线l:x=2
,0),满足|PF|与点P到直线l:x=2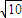 的距离之比为定值.
的距离之比为定值.
点评:本题考查用待定系数法求椭圆的标准方程,两个向量坐标形式的运算,以及椭圆的第二定义.
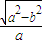 =
=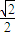 ,
,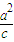 =
=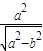 =2
=2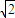 ,解出a、b 的值,即得椭圆的标准方程.
,解出a、b 的值,即得椭圆的标准方程.(Ⅱ)设动点P(x,y),M(x1,y1 )、N(x2,y2 ). 由向量间的关系得到 x=x1+2x2,y=y1+2y2,据M、N是椭圆上的点可得 x2+2y2=20+4(x1x2+2y1y2 ).再根据直线OM与ON的斜率之积为-
 ,得到点P是椭圆 x2+2y2=20 上的点,根据椭圆的第二定义,存在点F(
,得到点P是椭圆 x2+2y2=20 上的点,根据椭圆的第二定义,存在点F(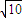 ,0),满足条件.
,0),满足条件.解答:解:(Ⅰ) 由题意得
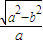 =
=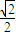 ,
,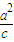 =
=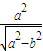 =2
=2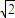 ,∴a=2,b=
,∴a=2,b=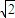 ,
,故椭圆的标准方程
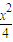 +
+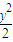 =1.
=1.(Ⅱ)设动点P(x,y),M(x1,y1 )、N(x2,y2 ).∵动点P满足:
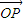 =
=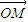 +2
+2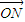 ,
,∴(x,y)=(x1+2x2,y1+2y2 ),∴x=x1+2x2,y=y1+2y2,
∵M、N是椭圆上的点,∴x12+2y12-4=0,x22+2y22-4=0.
∴x2+2y2=(x1+2x2)2+2 (y1+2y2)2=(x12+2y12 )+4(x22+2y22 )+4(x1x2+2y1y2 )
=4+4×4+4(x1x2+2y1y2 )=20+4(x1x2+2y1y2 ).
∵直线OM与ON的斜率之积为-
 ,∴
,∴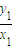 •
•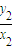 =-
=- ,∴x2+2y2=20,
,∴x2+2y2=20,故点P是椭圆
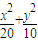 =1 上的点,焦点F(
=1 上的点,焦点F(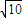 ,0),准线l:x=2
,0),准线l:x=2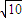 ,离心率为
,离心率为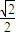 ,
,根据椭圆的第二定义,|PF|与点P到直线l:x=2
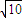 的距离之比为定值
的距离之比为定值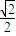 ,
,故存在点F(
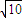 ,0),满足|PF|与点P到直线l:x=2
,0),满足|PF|与点P到直线l:x=2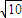 的距离之比为定值.
的距离之比为定值.点评:本题考查用待定系数法求椭圆的标准方程,两个向量坐标形式的运算,以及椭圆的第二定义.

练习册系列答案
相关题目
 如图,椭圆的中心为原点0,离心率e=
如图,椭圆的中心为原点0,离心率e=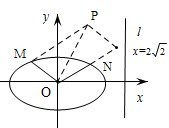 如图,椭圆的中心为原点O,离心率e=
如图,椭圆的中心为原点O,离心率e=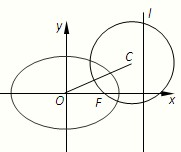 如图,椭圆的中心为原点O,已知右准线l的方程为x=4,右焦点F到它的距离为2.
如图,椭圆的中心为原点O,已知右准线l的方程为x=4,右焦点F到它的距离为2.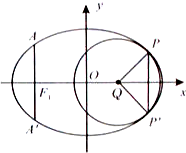 (2013•重庆)如图,椭圆的中心为原点O,长轴在x轴上,离心率
(2013•重庆)如图,椭圆的中心为原点O,长轴在x轴上,离心率