摘要:当时.点A.B的坐标为.这时点P的坐标为(0.0)也满足⑧.所以点P的轨迹方程为
网址:http://m.1010jiajiao.com/timu_id_20501[举报]
已知定点R的坐标为(0,-3),点P在x轴上,
⊥
,线段PM与y轴交于点Q,且满足
=2
(1)若点P在x轴上运动,求点M的轨迹E;
(2)求轨迹E的倾斜角为
的切线l0的方程;
(3)若(2)中切线l0与y轴交于点G,过G的直线l与轨迹E交于A、B两点,点D的坐标为(0,1),当∠ADB为钝角时,求直线l的斜率的取值范围.
查看习题详情和答案>>
| PR |
| PM |
| QM |
| PQ |
(1)若点P在x轴上运动,求点M的轨迹E;
(2)求轨迹E的倾斜角为
| π |
| 4 |
(3)若(2)中切线l0与y轴交于点G,过G的直线l与轨迹E交于A、B两点,点D的坐标为(0,1),当∠ADB为钝角时,求直线l的斜率的取值范围.
 如图,定点A,B的坐标分别为A(0,27),B(0,3),一质点C从原点出发,始终沿x轴的正方向运动,已知第1分钟内,质点C运动了1个单位,之后每分钟内比上一分钟内多运动了2个单位,记第n分钟内质点运动了an个单位,此时质点的位置为(Cn,0).
如图,定点A,B的坐标分别为A(0,27),B(0,3),一质点C从原点出发,始终沿x轴的正方向运动,已知第1分钟内,质点C运动了1个单位,之后每分钟内比上一分钟内多运动了2个单位,记第n分钟内质点运动了an个单位,此时质点的位置为(Cn,0).(Ⅰ)求an、Cn的表达式;
(Ⅱ)当n为何值时,tan∠ACnB取得最大,最大值为多少?
如图,定点A,B的坐标分别为A(0,27),B(0,3),一质点C从原点出发,始终沿x轴的正方向运动,已知第1分钟内,质点C运动了1个单位,之后每分钟内比上一分钟内多运动了2个单位,记第n分钟内质点运动了an个单位,此时质点的位置为(Cn,0).
(Ⅰ)求an、Cn的表达式;
(Ⅱ)当n为何值时,tan∠ACnB取得最大,最大值为多少?
 查看习题详情和答案>>
查看习题详情和答案>>
(Ⅰ)求an、Cn的表达式;
(Ⅱ)当n为何值时,tan∠ACnB取得最大,最大值为多少?
 查看习题详情和答案>>
查看习题详情和答案>>
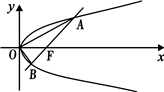 过直角坐标平面xOy中的抛物线y2=2px(p>0)的焦点F作一条倾斜角为
过直角坐标平面xOy中的抛物线y2=2px(p>0)的焦点F作一条倾斜角为