题目内容
已知定点R的坐标为(0,-3),点P在x轴上,
⊥
,线段PM与y轴交于点Q,且满足
=2
(1)若点P在x轴上运动,求点M的轨迹E;
(2)求轨迹E的倾斜角为
的切线l0的方程;
(3)若(2)中切线l0与y轴交于点G,过G的直线l与轨迹E交于A、B两点,点D的坐标为(0,1),当∠ADB为钝角时,求直线l的斜率的取值范围.
| PR |
| PM |
| QM |
| PQ |
(1)若点P在x轴上运动,求点M的轨迹E;
(2)求轨迹E的倾斜角为
| π |
| 4 |
(3)若(2)中切线l0与y轴交于点G,过G的直线l与轨迹E交于A、B两点,点D的坐标为(0,1),当∠ADB为钝角时,求直线l的斜率的取值范围.
分析:(1)设点M、P、Q的坐标分别为 (x,y)、(x1,0)、(0,y2),其中x1≠0.由向量数量积的坐标运算列式化简得x12-x1x-3y=0,根据
=2
得x1=-
,代入上式并化简整理,即可得到点M的轨迹E所表示的图形;
(2)利用导数求出l0的斜率为
x0,从而得到x0=2,再代入抛物线方程得切点为 (2,1),根据直线方程的点斜式列式,化简即得切线l0的方程;
(3)设A(x1,y1),B(x2,y2),求出直线l的方程并与抛物线方程消去y得关于x的一元二次方程,利用根与系数的关系列式得
,且△=16k2-16>0.根据∠ADB为钝角可得
•
<0,将
•
表示成关于x1+x2、x1x2和k的式子,化简整理得到关于k的二次不等式,解之即可得到直线l的斜率k的取值范围.
| QM |
| PQ |
| x |
| 2 |
(2)利用导数求出l0的斜率为
| 1 |
| 2 |
(3)设A(x1,y1),B(x2,y2),求出直线l的方程并与抛物线方程消去y得关于x的一元二次方程,利用根与系数的关系列式得
|
| DA |
| DB |
| DA |
| DB |
解答:解:(1)设点M的坐标为 (x,y),点P的坐标为 (x1,0)(x1≠0),点Q的坐标为(0,y2),
则
=(-x1,-3),
=(x-x1,y),
=(-x1,y2)
∵
⊥
,可得
•
=0,
∴-x1(x-x1)-3y=0,即x12-x1x-3y=0.
由
=2
得
=
,
∴将x1=-
代入上式,化简得y=
x2 (x≠0),
由此可得点M的轨迹E是抛物线y=
x2,除顶点外的图形;
(2)设切点为 (x0,y0),
∵求导数,得y'=
x,
∴切线l0的斜率为
x0=tan
=1,解之得x0=2,
代入抛物线方程得切点为 (2,1)
∴切线l0的方程为y-1=x-2,化简得x-y-1=0;
(3)∵l0的切线方程为x-y-1=0,∴令x=0,得x=-1,得G的坐标为(0,-1).
设l的斜率为k,得l的方程为y=kx-1.
由
消去y,得x2-4kπ+4=0.…①
设A(x1,y1),B(x2,y2),则x1,x2是方程①的两根,
∴
且△=16k2-16>0,解之得k2>1,
∵∠ADB为钝角,∴
.
由
=(x1,y1-1),
=(x2,y2-1).
可得:
•
=x1•x2+(y1-1)(y2-1)<0,即x1x2+(k x1-2)(kx2-2)<0,
∴x1x2+k2x1x2-2k(x1+x2)+4<0,化简得k2-2>0,解之得k<-
或k>
.
则
| PR |
| PM |
| PQ |
∵
| PR |
| PM |
| PR |
| PM |
∴-x1(x-x1)-3y=0,即x12-x1x-3y=0.
由
| QM |
| PQ |
| PQ |
| 1 |
| 2 |
| QM |
∴将x1=-
| x |
| 2 |
| 1 |
| 4 |
由此可得点M的轨迹E是抛物线y=
| 1 |
| 4 |
(2)设切点为 (x0,y0),
∵求导数,得y'=
| 1 |
| 2 |
∴切线l0的斜率为
| 1 |
| 2 |
| π |
| 4 |
代入抛物线方程得切点为 (2,1)
∴切线l0的方程为y-1=x-2,化简得x-y-1=0;
(3)∵l0的切线方程为x-y-1=0,∴令x=0,得x=-1,得G的坐标为(0,-1).
设l的斜率为k,得l的方程为y=kx-1.
由
|
设A(x1,y1),B(x2,y2),则x1,x2是方程①的两根,
∴
|
∵∠ADB为钝角,∴
|
由
| DA |
| DB |
可得:
| DA |
| DB |
∴x1x2+k2x1x2-2k(x1+x2)+4<0,化简得k2-2>0,解之得k<-
| 2 |
| 2 |
点评:本题求动点的轨迹方程,求曲线的切线并讨论直线的夹角为钝角的问题.着重考查了抛物线的几何性质、直线与圆锥曲线的关系、曲线的切线求法和向量的数量积等知识,属于中档题.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
 ,②
,② =
= =
=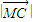 ,③
,③ ∥
∥
 ,0),已知
,0),已知 ∥
∥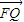 ,
,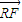 ∥
∥ 且
且 •
• =0.求四边形PRQN面积S的最大值和最小值.
=0.求四边形PRQN面积S的最大值和最小值.