摘要:得M(1..0)..
网址:http://m.1010jiajiao.com/timu_id_20118[举报]
(1)若m,n∈R,由m2+n2≥2mn可得2(m2+n2)≥m2+n2+2mn,即有2(m2+n2)≥(m+n)2;
(2)已知x>0,y>0,且x+y=1,利用(1)中不等式,求
+
的最大值并求出对应的x,y的值.
查看习题详情和答案>>
(2)已知x>0,y>0,且x+y=1,利用(1)中不等式,求
x+
|
y+
|
(1)请写出一个各项均为实数且公比0<q<1的等比数列,使得其同时满足a1+a6=11且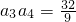 ;
;
(2)在符合(1)条件的数列中,能否找到一正偶数m,使得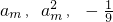 这三个数依次成等差数列?若能,求出这个m的值; 若不能,请说明理由.
这三个数依次成等差数列?若能,求出这个m的值; 若不能,请说明理由.
查看习题详情和答案>>
(1)椭圆C: (a>b>0)与x轴交于A、B两点,点P是椭圆C上异于A、B的任意一点,直线PA、PB分别与y轴交于点M、N,求证:
(a>b>0)与x轴交于A、B两点,点P是椭圆C上异于A、B的任意一点,直线PA、PB分别与y轴交于点M、N,求证: 为定值b2-a2。
为定值b2-a2。
(2)由(1)类比可得如下真命题:双曲线C: (a>0,b>0)与x轴交于A、B两点,点P是双曲线C上异于A、B的任意一点,直线PA、PB分别与y轴交于点M、N,则
(a>0,b>0)与x轴交于A、B两点,点P是双曲线C上异于A、B的任意一点,直线PA、PB分别与y轴交于点M、N,则 为定值,请写出这个定值(不要求给出解题过程)。
为定值,请写出这个定值(不要求给出解题过程)。
查看习题详情和答案>>
 (a>b>0)与x轴交于A、B两点,点P是椭圆C上异于A、B的任意一点,直线PA、PB分别与y轴交于点M、N,求证:
(a>b>0)与x轴交于A、B两点,点P是椭圆C上异于A、B的任意一点,直线PA、PB分别与y轴交于点M、N,求证: 为定值b2-a2。
为定值b2-a2。(2)由(1)类比可得如下真命题:双曲线C:
 (a>0,b>0)与x轴交于A、B两点,点P是双曲线C上异于A、B的任意一点,直线PA、PB分别与y轴交于点M、N,则
(a>0,b>0)与x轴交于A、B两点,点P是双曲线C上异于A、B的任意一点,直线PA、PB分别与y轴交于点M、N,则 为定值,请写出这个定值(不要求给出解题过程)。
为定值,请写出这个定值(不要求给出解题过程)。 +
+ 的最大值并求出对应的x,y的值.
的最大值并求出对应的x,y的值.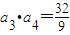 ;
;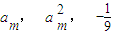 这三个数依次成等差数列?若能,求出这个m的值; 若不能,请说明理由.
这三个数依次成等差数列?若能,求出这个m的值; 若不能,请说明理由.