题目内容
(1)若m,n∈R,由m2+n2≥2mn可得2(m2+n2)≥m2+n2+2mn,即有2(m2+n2)≥(m+n)2;(2)已知x>0,y>0,且x+y=1,利用(1)中不等式,求
 +
+ 的最大值并求出对应的x,y的值.
的最大值并求出对应的x,y的值.
【答案】分析:利用题中给出的不等式2(m2+n2)≥(m+n)2,结合条件x+y=1,构造出不等关系 ,即可求出答案.
,即可求出答案.
解答:解: …(3分)
…(3分)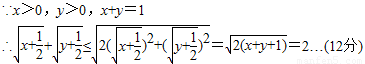
∴ ,
,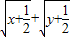 有最大值2…(14分)
有最大值2…(14分)
点评:本题主要考查了不等式的证明,考查了利用基本不等式求最值,属于基础题.
 ,即可求出答案.
,即可求出答案.解答:解:
 …(3分)
…(3分)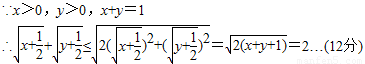
∴
 ,
,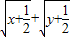 有最大值2…(14分)
有最大值2…(14分)点评:本题主要考查了不等式的证明,考查了利用基本不等式求最值,属于基础题.

练习册系列答案
相关题目