摘要：由为锐角三角形得． ---3分
网址：http://m.1010jiajiao.com/timu_id_200004[举报]
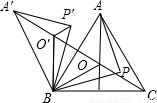
如图，O是锐角三角形ABC内一点，∠AOB=∠BOC=∠COA=120°，P是△ABC内不同于O的另一点；△A′BO′，△A′BP′分别由△AOB，△APB旋转而得，旋转角都为60°，则下列结论中正确的有（ ）
①△O′BO为等边三角形，且A′，O′，O，C在一条直线上．
②A′O′+O′O=AO+BO．
③A′P′+P′P=PA+PB．
④PA+PB+PC＞AO+BO+CO．
A．1个
B．2个
C．3个
D．4个
查看习题详情和答案>>
①△O′BO为等边三角形，且A′，O′，O，C在一条直线上．
②A′O′+O′O=AO+BO．
③A′P′+P′P=PA+PB．
④PA+PB+PC＞AO+BO+CO．
A．1个
B．2个
C．3个
D．4个
查看习题详情和答案>>
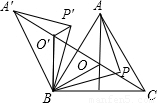
如图，O是锐角三角形ABC内一点，∠AOB=∠BOC=∠COA=120°，P是△ABC内不同于O的另一点；△A′BO′，△A′BP′分别由△AOB，△APB旋转而得，旋转角都为60°，则下列结论中正确的有（ ）
①△O′BO为等边三角形，且A′，O′，O，C在一条直线上．
②A′O′+O′O=AO+BO．
③A′P′+P′P=PA+PB．
④PA+PB+PC＞AO+BO+CO．
A．1个
B．2个
C．3个
D．4个
查看习题详情和答案>>
①△O′BO为等边三角形，且A′，O′，O，C在一条直线上．
②A′O′+O′O=AO+BO．
③A′P′+P′P=PA+PB．
④PA+PB+PC＞AO+BO+CO．
A．1个
B．2个
C．3个
D．4个
查看习题详情和答案>>
如图①，直角三角形的两个锐角分别是40°和50°，其三边上分别有一个正方形．执行下面的操作：由两个小正方形向外分别作锐角为40°和50°的直角三角形，再分别以所得到的直角三角形的直角边为边长作正方形．图②是一次操作后的图形．
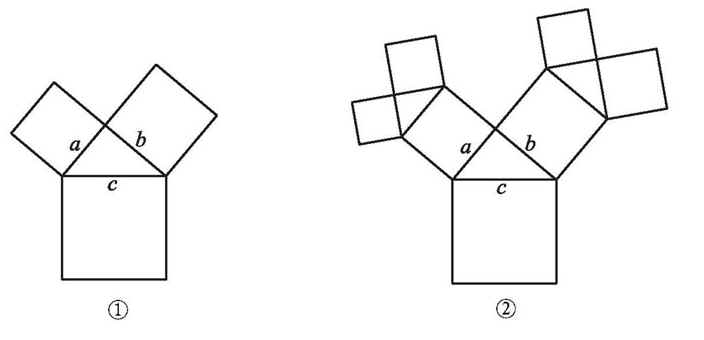
(1)试画出2次操作后的图形．
(2)如果原来直角三角形斜边长为1厘米，写出2次操作后的图形中所有正方形的面积和．
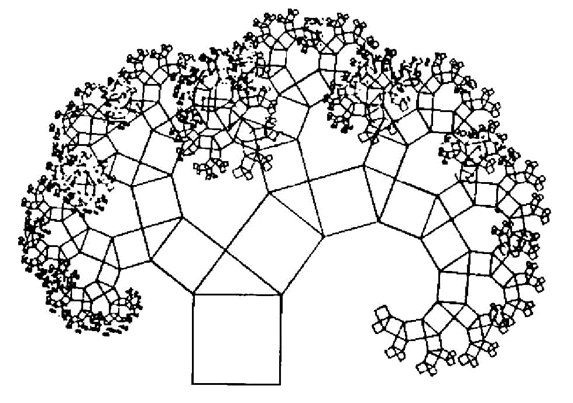
(3)如果一直画下去，你能想像出它的样子吗？
(4)下图是重复上述步骤若干次后得到的图形，人们把它称为“毕达哥拉斯树”．如果最初的直角三角形等腰直角三角形，你能想像出此时“毕达哥拉斯树”的形状吗？
的中点D、E，同时得到两条折痕DF、EG，分别沿折痕DF、EG剪下图中的三角形①、②，并按图中箭头所指的方向分别旋转180°．