题目内容
如图
1,直角三角形的两个锐角分别是40°和50°,其三边上分别有一个正方形.执行下面的操作:由两个小正方形向外分别作锐角为40°和50°的直角三角形,再分别以所得的直角三角形的直角边为边长作正方形.
(1)试画出1次操作后的图形;
(2)如果原来的直角三角形斜边长为1厘米,写出1次操作后的图形中所有正方形的面积和.
答案:
解析:
解析:
|
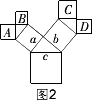
解题思路:观察如图 1,因为a、b、c分别是直角三角形的两条直角边和斜边,根据勾股定理,可得a2+b2=c2.又因为A、B、C分别是三个正方形的边长,所以a2、b2、c2分别是三个正方形的面积.由此可得到以a、b为边的两个正方形的面积之和等于以c为边长的正方形的面积.1次操作后如图2所示,从图形中找出基本图形(如图1),根据基本图形中三个正方形的面积满足的关系可得,正方形A与正方形B的面积之和等于a2,正方形C与正方形D的面积之和等于b2,然后再根据a2+b2=c2,可得正方形A、B、C、D的面积之和等于c2.只要知道C的值,就可求出正方形A、B、C、D的面积和.
命题意图:本题主要借助勾股定理的图形证明进行变式训练,提高同学们分析问题、解决问题的能力以及探究能力. |

练习册系列答案
相关题目
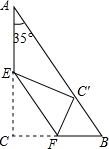 如图是一个直角三角形的纸片,将直角沿EF折叠,使C点落在AB边上,并且使∠EC′A=∠A,那么∠C′FE的度数是( )
如图是一个直角三角形的纸片,将直角沿EF折叠,使C点落在AB边上,并且使∠EC′A=∠A,那么∠C′FE的度数是( )| A、50° | B、45° | C、55° | D、70°第7题图 |
 7、如图,以直角三角形的三边为边向三角形外作正方形,已知甲、乙两个正方形的面积分别为4、6,则丙正方形的面积为
7、如图,以直角三角形的三边为边向三角形外作正方形,已知甲、乙两个正方形的面积分别为4、6,则丙正方形的面积为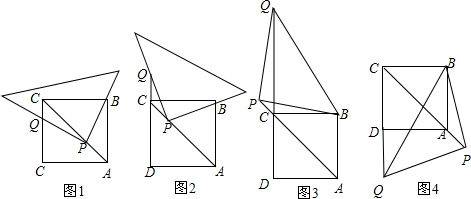
 如图,一个直角三角形的三边长均为正整数,已知它的一条直角边的长恰是3,那么另一条直角边的长是
如图,一个直角三角形的三边长均为正整数,已知它的一条直角边的长恰是3,那么另一条直角边的长是 如图,以直角三角形的两条直角边AC、AB为直径,向三角形内作半圆,两半圆交于点D,CD=1,BD=3,则图中阴影部分的面积为
如图,以直角三角形的两条直角边AC、AB为直径,向三角形内作半圆,两半圆交于点D,CD=1,BD=3,则图中阴影部分的面积为