网址:http://m.1010jiajiao.com/timu_id_198970[举报]
说明:1.参考答案与评分标准指出了每道题要考查的主要知识和能力,并给出了一种或几种解法供参考,如果考生的解法与参考答案不同,可根据试题主要考查的知识点和能力比照评分标准给以相应的分数.
2.对解答题中的计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的得分,但所给分数不得超过该部分正确解答应得分数的一半;如果后继部分的解答有较严重的错误,就不再给分.
3.解答右端所注分数,表示考生正确做到这一步应得的累加分数.
4.只给整数分数,选择题和填空题不给中间分.
一、选择题:本大题考查基本知识和基本运算.共10小题,每小题5分,满分50分.
题号
1
2
3
4
5
6
7
8
9
10
答案
B
A
C
C
D
A
B
D
C
B
二、填空题:本大题共5小题,每小题5分,满分20分.其中14~15题是选做题,考生只能选做一题,两题全答的,只计算前一题得分.第13题第1个空3分,第2个空2分.
11.0
12.79
13.文科数学.files/image259.gif) ,
,文科数学.files/image261.gif) 14.1
15.6
14.1
15.6
三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.
16.(本小题主要考查三角函数性质和三角函数的基本关系等知识,考查化归与转化的数学思想方法,以及运算求解能力)
解:(1)文科数学.files/image263.gif)
文科数学.files/image265.gif) .
.
∵文科数学.files/image267.gif)
文科数学.files/image269.gif) R,
R,
∴函数文科数学.files/image034.gif) 的值域为
的值域为文科数学.files/image271.gif) .
.
(2)∵文科数学.files/image158.gif) ,
,文科数学.files/image160.gif) ,
,
∴文科数学.files/image273.gif) ,
,文科数学.files/image275.gif) .
.
∵文科数学.files/image277.gif) 都是锐角,
都是锐角,
∴文科数学.files/image279.gif) ,
,文科数学.files/image281.gif) .
.
∴文科数学.files/image283.gif)
文科数学.files/image285.gif)
文科数学.files/image287.gif)
∴文科数学.files/image162.gif) 的值为
的值为文科数学.files/image290.gif) .
.
17.(本小题主要考查古典概型等基础知识,考查化归和转化、分类与整合的数学思想方法,以及简单的推理论证能力)
解:由于实数对文科数学.files/image292.gif) 的所有取值为:
的所有取值为:文科数学.files/image294.gif) ,
,文科数学.files/image296.gif) ,
,文科数学.files/image298.gif) ,
,文科数学.files/image300.gif) ,
,文科数学.files/image302.gif) ,
,文科数学.files/image304.gif) ,
,文科数学.files/image306.gif) ,
,文科数学.files/image308.gif) ,
,文科数学.files/image310.gif) ,
,文科数学.files/image312.gif) ,
,文科数学.files/image067.gif) ,
,文科数学.files/image315.gif) ,
,文科数学.files/image317.gif) ,
,文科数学.files/image319.gif) ,
,文科数学.files/image321.gif) ,
,文科数学.files/image323.gif) ,共16种.
,共16种.
设“直线文科数学.files/image168.gif) 不经过第四象限”为事件
不经过第四象限”为事件文科数学.files/image126.gif) ,“直线
,“直线文科数学.files/image327.gif) 与圆
与圆文科数学.files/image171.gif) 有公共点”为事件
有公共点”为事件文科数学.files/image189.gif) .
.
(1)若直线文科数学.files/image168.gif) 不经过第四象限,则必须满足
不经过第四象限,则必须满足文科数学.files/image332.gif)
即满足条件的实数对文科数学.files/image334.gif) 有
有文科数学.files/image067.gif) ,
,文科数学.files/image315.gif) ,
,文科数学.files/image321.gif) ,
,文科数学.files/image323.gif) ,共4种.
,共4种.
∴文科数学.files/image340.gif) .
.
故直线文科数学.files/image168.gif) 不经过第四象限的概率为
不经过第四象限的概率为文科数学.files/image095.gif) .
.
(2)若直线文科数学.files/image327.gif) 与圆
与圆文科数学.files/image171.gif) 有公共点,则必须满足
有公共点,则必须满足文科数学.files/image344.gif) ≤1,即
≤1,即文科数学.files/image346.gif) ≤
≤文科数学.files/image348.gif) .
.
若文科数学.files/image350.gif) ,则
,则文科数学.files/image352.gif) 符合要求,此时实数对(
符合要求,此时实数对(文科数学.files/image354.gif) )有4种不同取值;
)有4种不同取值;
若文科数学.files/image356.gif) ,则
,则文科数学.files/image358.gif) 符合要求,此时实数对(
符合要求,此时实数对(文科数学.files/image354.gif) )有2种不同取值;
)有2种不同取值;
若文科数学.files/image360.gif) ,则
,则文科数学.files/image358.gif) 符合要求,此时实数对(
符合要求,此时实数对(文科数学.files/image354.gif) )有2种不同取值;
)有2种不同取值;
若文科数学.files/image363.gif) ,则
,则文科数学.files/image352.gif) 符合要求,此时实数对(
符合要求,此时实数对(文科数学.files/image354.gif) )有4种不同取值.
)有4种不同取值.
∴满足条件的实数对文科数学.files/image334.gif) 共有12种不同取值.
共有12种不同取值.
∴文科数学.files/image367.gif) .
.
故直线文科数学.files/image327.gif) 与圆
与圆文科数学.files/image171.gif) 有公共点的概率为
有公共点的概率为文科数学.files/image098.gif) .
.
18.(本小题主要考查空间线面关系、几何体的表面积与体积等知识,考查数形结合的数学思想方法,以及空间想象能力、运算求解能力)
(1)证法1:如图,连结文科数学.files/image370.gif) ,
,
文科数学.files/image372.jpg) ∵
∵文科数学.files/image181.gif) 是长方体,
是长方体,
∴文科数学.files/image375.gif) 且
且文科数学.files/image377.gif) .
.
∴四边形文科数学.files/image379.gif) 是平行四边形.
是平行四边形.
∴文科数学.files/image381.gif) .
.
∵文科数学.files/image383.gif) 平面
平面文科数学.files/image199.gif) ,
,文科数学.files/image385.gif) 平面
平面文科数学.files/image199.gif) ,
,
∴文科数学.files/image387.gif) 平面
平面文科数学.files/image199.gif) .
.
证法2:∵文科数学.files/image181.gif) 是长方体,
是长方体,
∴平面文科数学.files/image389.gif)
文科数学.files/image197.gif) 平面
平面文科数学.files/image199.gif) .
.
∵文科数学.files/image393.gif) 平面
平面文科数学.files/image389.gif) ,
,文科数学.files/image383.gif) 平面
平面文科数学.files/image199.gif) ,
,
∴文科数学.files/image387.gif) 平面
平面文科数学.files/image199.gif) .
.
(2)解:设文科数学.files/image396.gif) ,∵几何体
,∵几何体文科数学.files/image191.gif) 的体积为
的体积为文科数学.files/image193.gif) ,
,
∴文科数学.files/image398.gif) ,
,
即文科数学.files/image400.gif) ,
,
即文科数学.files/image402.gif) ,解得
,解得文科数学.files/image404.gif) .
.
∴文科数学.files/image201.gif) 的长为4.
的长为4.
(3)如图,连结文科数学.files/image406.gif) ,设
,设文科数学.files/image406.gif) 的中点为
的中点为文科数学.files/image408.gif) ,连
,连文科数学.files/image410.gif)
∵文科数学.files/image181.gif) 是长方体,∴
是长方体,∴文科数学.files/image413.gif) 平面
平面文科数学.files/image389.gif) .
.
∵文科数学.files/image393.gif) 平面
平面文科数学.files/image389.gif) ,∴
,∴文科数学.files/image413.gif)
文科数学.files/image195.gif) .
.
∴文科数学.files/image418.gif) .同理
.同理文科数学.files/image420.gif) .
.
∴文科数学.files/image422.gif) .
.
∴经过文科数学.files/image185.gif) ,
,文科数学.files/image187.gif) ,
,文科数学.files/image189.gif) ,
,文科数学.files/image427.gif) 四点的球的球心为点
四点的球的球心为点文科数学.files/image408.gif) .
.
∵文科数学.files/image430.gif) .
.
∴文科数学.files/image432.gif) .
.
故经过文科数学.files/image185.gif) ,
,文科数学.files/image187.gif) ,
,文科数学.files/image189.gif) ,
,文科数学.files/image427.gif) 四点的球的表面积为
四点的球的表面积为文科数学.files/image434.gif) .
.
19.(本小题主要考查椭圆、圆的方程和圆与圆的位置关系等基础知识,考查数形结合思想,以及运算求解能力)
解:(1)∵椭圆文科数学.files/image207.gif)
文科数学.files/image437.gif) 的离心率为
的离心率为文科数学.files/image078.gif) ,且经过点
,且经过点文科数学.files/image213.gif)
文科数学.files/image441.gif) ,
,
∴文科数学.files/image443.gif)
即文科数学.files/image445.gif) 解得
解得文科数学.files/image447.gif)
∴椭圆文科数学.files/image205.gif) 的方程为
的方程为文科数学.files/image450.gif) .
.
(2)∵文科数学.files/image452.gif) ,
,文科数学.files/image454.gif) ,∴
,∴文科数学.files/image456.gif) .
.
∴椭圆文科数学.files/image205.gif) 的左焦点坐标为
的左焦点坐标为文科数学.files/image459.gif) .
.
以椭圆文科数学.files/image205.gif) 的长轴为直径的圆的方程为
的长轴为直径的圆的方程为文科数学.files/image461.gif) ,圆心坐标是
,圆心坐标是文科数学.files/image463.gif) ,半径为2.
,半径为2.
以文科数学.files/image219.gif) 为直径的圆的方程为
为直径的圆的方程为文科数学.files/image466.gif) ,圆心坐标是
,圆心坐标是文科数学.files/image468.gif) ,半径为
,半径为文科数学.files/image470.gif) .
.
∵两圆心之间的距离为文科数学.files/image472.gif) ,
,
故以文科数学.files/image219.gif) 为直径的圆与以椭圆长轴为直径的圆内切.
为直径的圆与以椭圆长轴为直径的圆内切.
20.(本小题主要考查等差数列、等比数列的通项公式与前文科数学.files/image102.gif) 项求和公式等知识,考查化归与转化、分类与整合的数学思想方法,以及推理论证能力和运算求解能力)
项求和公式等知识,考查化归与转化、分类与整合的数学思想方法,以及推理论证能力和运算求解能力)
解:设等比数列文科数学.files/image221.gif) 的首项为
的首项为文科数学.files/image476.gif) ,公比为
,公比为文科数学.files/image478.gif)
文科数学.files/image480.gif) ,
,
若文科数学.files/image226.gif) ,
,文科数学.files/image228.gif) ,
,文科数学.files/image230.gif) 成等差数列,
成等差数列,
则文科数学.files/image482.gif)
文科数学.files/image484.gif)
文科数学.files/image230.gif) .
.
∴文科数学.files/image486.gif) .
.
∵文科数学.files/image488.gif) ,
,文科数学.files/image490.gif) ,∴
,∴文科数学.files/image492.gif) .
.
解得文科数学.files/image494.gif) 或
或文科数学.files/image496.gif) .
.
当文科数学.files/image494.gif) 时,∵
时,∵文科数学.files/image498.gif) ,
,文科数学.files/image500.gif) ,
,文科数学.files/image502.gif) ,
,
∴文科数学.files/image504.gif) .
.
∴当文科数学.files/image494.gif) 时,
时,文科数学.files/image234.gif) ,
,文科数学.files/image236.gif) ,
,文科数学.files/image238.gif) 不成等差数列.
不成等差数列.
当文科数学.files/image496.gif) 时,
时,文科数学.files/image234.gif) ,
,文科数学.files/image507.gif) ,
,文科数学.files/image509.gif) 成等差数列.下面给出两种证明方法.
成等差数列.下面给出两种证明方法.
证法1:∵文科数学.files/image511.gif)
文科数学.files/image513.gif)
文科数学.files/image515.gif)
文科数学.files/image517.gif)
文科数学.files/image519.gif) ,
,
∴文科数学.files/image521.gif) .
.
∴当文科数学.files/image496.gif) 时,
时,文科数学.files/image234.gif) ,
,文科数学.files/image236.gif) ,
,文科数学.files/image238.gif) 成等差数列.
成等差数列.
证法2:∵文科数学.files/image523.gif) ,
,
又文科数学.files/image525.gif)
文科数学.files/image527.gif)
文科数学.files/image529.gif) ,
,
∴文科数学.files/image521.gif) .
.
∴当文科数学.files/image496.gif) 时,
时,文科数学.files/image234.gif) ,
,文科数学.files/image236.gif) ,
,文科数学.files/image238.gif) 成等差数列.
成等差数列.
21.(本小题主要考查函数的性质、函数与导数等知识,考查化归与转化、分类与整合的数学思想方法,以及抽象概括能力、推理论证能力和运算求解能力)
(1)解法1:∵文科数学.files/image531.gif) ,其定义域为
,其定义域为文科数学.files/image533.gif) ,
,
∴文科数学.files/image535.gif) .
.
∵文科数学.files/image070.gif) 是函数
是函数文科数学.files/image538.gif) 的极值点,
的极值点,
∴文科数学.files/image540.gif) ,即
,即文科数学.files/image542.gif) ,
,
∵文科数学.files/image244.gif) ,∴
,∴文科数学.files/image545.gif) .
.
经检验,当文科数学.files/image545.gif) 时,
时,文科数学.files/image056.gif) =1是函数
=1是函数文科数学.files/image548.gif) 的极值点,
的极值点,
∴文科数学.files/image545.gif) . ?
. ?
解法2:∵文科数学.files/image531.gif) ,其定义域为
,其定义域为文科数学.files/image533.gif) ,
,
∴文科数学.files/image535.gif) .
.
令文科数学.files/image550.gif) ,即
,即文科数学.files/image552.gif) ,整理得,
,整理得,文科数学.files/image554.gif) .
.
∵文科数学.files/image556.gif) ,
,
∴文科数学.files/image550.gif) 的两个实根
的两个实根文科数学.files/image558.gif) (舍去),
(舍去),文科数学.files/image560.gif) ,
,
当文科数学.files/image056.gif) 变化时,
变化时,文科数学.files/image538.gif) ,
,文科数学.files/image564.gif) 的变化情况如下表:
的变化情况如下表:
文科数学.files/image056.gif)
文科数学.files/image567.gif)
文科数学.files/image569.gif)
椭圆 的方程为
的方程为 ,离心率为
,离心率为 ,且短轴一端点和两焦点构成的三角形面积为1,抛物线
,且短轴一端点和两焦点构成的三角形面积为1,抛物线 的方程为
的方程为 ,抛物线的焦点F与椭圆的一个顶点重合.
,抛物线的焦点F与椭圆的一个顶点重合.
(1)求椭圆 和抛物线
和抛物线 的方程;
的方程;
(2)过点F的直线交抛物线 于不同两点A,B,交y轴于点N,已知
于不同两点A,B,交y轴于点N,已知 的值.
的值.
(3)直线 交椭圆
交椭圆 于不同两点P,Q,P,Q在x轴上的射影分别为P′,Q′,满足
于不同两点P,Q,P,Q在x轴上的射影分别为P′,Q′,满足 (O为原点),若点S满足
(O为原点),若点S满足 ,判定点S是否在椭圆
,判定点S是否在椭圆 上,并说明理由.
上,并说明理由.
 的方程为
的方程为 ,离心率为
,离心率为 ,且短轴一端点和两焦点构成的三角形面积为1,抛物线
,且短轴一端点和两焦点构成的三角形面积为1,抛物线 的方程为
的方程为 ,抛物线的焦点F与椭圆的一个顶点重合.
,抛物线的焦点F与椭圆的一个顶点重合.(1)求椭圆
 和抛物线
和抛物线 的方程;
的方程;(2)过点F的直线交抛物线
 于不同两点A,B,交y轴于点N,已知
于不同两点A,B,交y轴于点N,已知 的值.
的值.(3)直线
 交椭圆
交椭圆 于不同两点P,Q,P,Q在x轴上的射影分别为P′,Q′,满足
于不同两点P,Q,P,Q在x轴上的射影分别为P′,Q′,满足 (O为原点),若点S满足
(O为原点),若点S满足 ,判定点S是否在椭圆
,判定点S是否在椭圆 上,并说明理由.
上,并说明理由.




 为椭圆上任意一点,以
为椭圆上任意一点,以 为半径作圆
为半径作圆 有公共点时,求△
有公共点时,求△ 面积的最大值
面积的最大值 ,斜率为1的直线不经过原点
,斜率为1的直线不经过原点 ,而且与椭圆相交于
,而且与椭圆相交于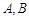 两点,
两点, 为线段
为线段 的中点.
的中点. 与
与 之间满足的关系式;若不能,说明理由;
之间满足的关系式;若不能,说明理由; 的中点,且
的中点,且 点在椭圆上.若
点在椭圆上.若 ,求
,求 ,斜率为1的直线不经过原点
,斜率为1的直线不经过原点 ,而且与椭圆相交于
,而且与椭圆相交于 两点,
两点, 为线段
为线段 的中点.
的中点. 与
与 之间满足什么关系;若不能,说明理由;
之间满足什么关系;若不能,说明理由; 的中点,且
的中点,且 点在椭圆上.若
点在椭圆上.若 ,求椭圆的离心率.
,求椭圆的离心率.